Если начало координат на рис.1.5 перенести в точку при i=-I0, то кривая намагничивания становиться аналогичной кривой намагничивания двигателя с последовательным возбуждением. Следовательно, линия i=-I0 является асимптотой для электромеханической характеристики двигателя смешанного возбуждения (рис.1.6). Скорость идеального холостого хода
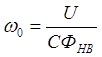 (1.19)
(1.19)
реализуется за счет независимого возбуждения.
Так как для двигателей смешанного возбуждения Фнв=(0,7…0,85)Фн, то w0=(1.2…1.6)wН.
Механическая характеристика по форме отличается от электромеханической характеристики. Так как
М=С(Фнв+Фпв)I, (1.20)
то как при I=0, так и при Фнв+Фпв=0 (чему соответствует условие i=-I0), развиваемый двигателем электромагнитный момент равен нулю, а при –I0<i<0, когда Фнв+Фпв>0, двигатель работает, развивая электромагнитный момент с отрицательным знаком (рис.1.7). максимальное значение этого момента ММ невелико и обычно не превышает 10% от номинального значения электромагнитного момента.
 |
|||
|
|||
1.5 Характеристики асинхронных двигателей в установившихся режимах.
В двигательном режиме двигатель потребляет из сети активную мощность.
Р1=3U1I1Cosj1. (1.21)
Здесь U1, I1 – соответственно эффективные значения j1 – угол сдвига между векторами ![]() 1
и
1
и ![]() 1.
1.
Часть потребляемой мощности теряется в активном сопротивлении r1 обмотки статора в виде электрических потерь:
DРЭ,1=3r1I12. (1.22)
Также теряется энергия в сердечнике статора в виде магнитных потерь DPмг,1.
Разность
Рэм=Р1+DРэ,1-DРмг,1 (1.23)
 |
представляет собой электромагнитную мощность, передаваемую посредством магнитного поля со статора на ротор. На схеме замещения (рис.1.8) этой мощности соответствует мощность в активном сопротивлении ротора r2’/s:
Рэм=3(I2’)2r2’/s. (1/24)
Часть этой мощности теряется в виде электрических потерь в активном сопротивлении ротора:
DРэ,г=3(I2’)2r2’. (1.25)
Разность Рэм-DРэ,г является развиваемой двигателем механической мощностью:
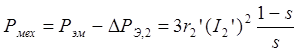 .
(1.26)
.
(1.26)
С другой стороны, механическая мощность определяется произведением электромагнитного момента и скорости вращения ротора:
Рмех=Мw. (1.27)
Так как
w=(1-s)w1 (1.28)
Где w1 – скорость вращения магнитного поля, то из равенства правых частей выражений (1.26) и (1.27) следует:
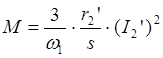 (1.29)
(1.29)
Из схемы замещения (рис.1.8)
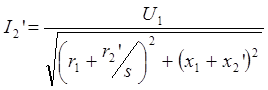 (1.30)
(1.30)
Тогда
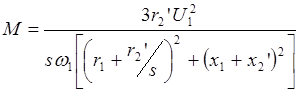 .
(1.31)
.
(1.31)
Анализ функции M(s) показывает:
· При s>0 также M>0;
· При s<0 также M<0;
· При s=0 также M=0;
· При s®±¥ M=0;
· функция (1.31) имеет экстремумы.
Для определения экстремумов функцию (1.31) представим в следующем виде:
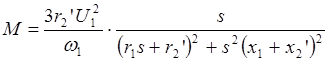 .
.
Тогда
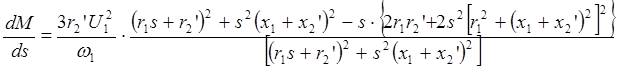 .
(1.32)
.
(1.32)
Экстремумам существует условие: dM/ds=0. Условие удовлетворяется в том случае, когда числитель выражения (1.32) равен нулю. Следовательно, обозначив скольжения, при которых достигаются максимальные значения электромагнитного момента, как sкр, запишем:
![]() .
.
Отсюда находим:
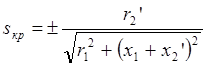 .
(1.33)
.
(1.33)
При подстановке (1.33) в (1.31) определяем экстремальные (критические) значения момента:
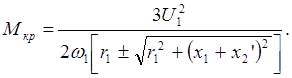 (1.34)
(1.34)
В выражениях (1.33), (1.34) знаки плюс относятся к двигательному, а знаки минус – к генераторному режимам работы двигателя. В практических расчетах удобно использовать представление электромагнитного момента как функцию критического момента.
Из (1.31) и (1.34) следует, что

Учитывая, что
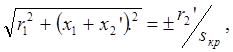


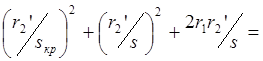
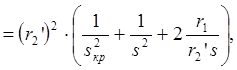
получим:

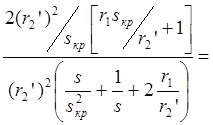
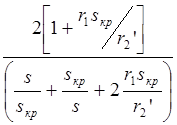 (1.35)
(1.35)
Формула
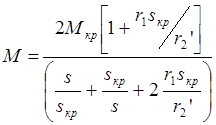 (1.36)
(1.36)
получила специальное название «формула Клосса».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.