Управление режимами работы электрических двигателей в разомкнутых системах электропривода. Модели двигателей в установившихся режимах, страница 11

                    (3.27)

При изменении напряжения машина не размагнитится и сохранит работоспособность, если Dw_с<w_с. с учетом (3.27) это условие преобразуется к виду

U²-4r_aM_cw_c>0.

Следовательно, при заданных значениях М_с, w_с можно обеспечить реализуемость режима, если

U>U_мин=2.                    (3.28)

Теперь можно предположить следующую процедуру определения необходимого уровня напряжения:

·  Задать некоторое значение напряжения из интервала U_мин<U<U_н;

·  Определить из (3.24) значение I_c,1;

·  По кривой намагничивания найти значение СФ(I_с), соответствующее I_c,1;

·  Из (3.23) определить значение (СФ)₁.

Если найденные двумя способами значения СФ совпадают, то заданное значение напряжения равно требуемому значению. В противном случае повторить вычисления для другого значения U.

3.7  Регулирование скорости двигателя постоянного тока с последовательным возбуждением изменением сопротивления якорной цепи.

При изменении сопротивления якорной цепи отклонение скорости, как и для двигателя с независимым возбуждением, изменяется пропорционально R_a=r_a+r_a,доб, где r_a,доб – добавочное сопротивление.

Для расчета сопротивления, включение которого обеспечивает работу с заданной скоростью w_с при заданной нагрузке на валу можно использовать следующий способ.

При известной кривой намагничивания ток I_с, с которым двигатель будет работать в установившемся режиме, можно определить итерационным методом, задавая различные значения тока, и определяя создаваемый при этом поток, проверяя далее выполнение условия М_с=СФ(I_c)I_c. После определения I_c значение R_а определяется просто:

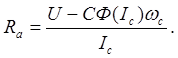                    (3.29)

3.8  Регулирование скорости двигателя постоянного тока с последовательным возбуждением в схемах шунтирования якоря.

Возможны три варианта схем шунтирования (рис.3.9). первая схема (рис.3.9,а) не устраняет основной недостаток двигателя с последовательным возбуждением – отсутствие режима холостого хода при конечной (невысокой) скорости – и работоспособна только при наличии нагрузки на валу. Поэтому схему не анализируем.

 

Схема, приведенная на рис.3.9,б может обеспечивать режим идеального холостого хода при конечной регулируемой скорости, имеет наилучшее по сравнению с другими схемами возможности для регулирования скорости в двигательном режиме. Для нее справедливы выражения (3.12), (3.13) для механической и электромеханической характеристик.

Скорость идеального холостого хода

                      (3.30)

можно регулировать изменением соотношения между сопротивлениями

При любой скорости

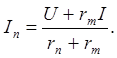                         (3.31)

Следовательно, при

I=-U/r_m                        (3.32)

машина размагничивается и скорость двигателя неограниченно возрастает (рис.3.10,а). Момент двигателя при этом стремиться к нулю (рис.3.10,б). Следовательно, в рассмотренном случае двигатель с последовательным возбуждением приобретает свойства, присущие  двигателю со смешанным возбуждением.

Для расчета сопротивлений, обеспечивающих работу двигателя со скоростью w_с при моменте сопротивления М_с, можно использовать метод, рассмотренный в п.3.5. Для этого нужно задаться значениями СФ и I₀, определить a, r_ш, r_п и по кривой намагничивания опрделить поток возбуждения. Если значение СФ , найденное по кривой намагничивания, совпадает с заданным значением СФ, расчет сопротивлений заканчивается. В противном случае нужно повторить вычисления задании другого значения СФ.

Схема, показанная на рис.3.9,в, при r_п=0 переводит двигатель в режим параллельного возбуждения. При r_п¹0 якорь двигателя оказывается подключенным к части делителя напряжения, образованного сопротивлениями r_ш и r_п. Возможен режим идеального холостого хода (3.11). схема позволяет осуществить плавный переход из двигательного режима в режим рекуперации.