Управление режимами работы электрических двигателей в разомкнутых системах электропривода. Модели двигателей в установившихся режимах, страница 10

 

Исходя из баланса напряжений и токов в установившихся режимах

U=r_mI_m+r_nI_n,

E+R_aI=r_mI_m,                                     (3.11)

I_n=I+I_m,

где R_a=r_a+r_a,доб, с учетом выражений (1.1), (1.3) получаем выражения, описывающие механические и электромеханические характеристики двигателя:

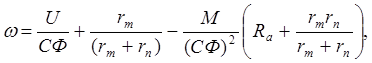             (3.12)

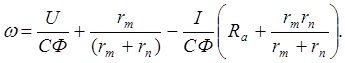               (3.13)

Из приведенных выражений следует, что при использовании рассматриваемой схемы имеется возможность изменения скорости и идеального холостого хода и жесткости характеристик (рис.3.8). Жесткость механической характеристики в данном случае

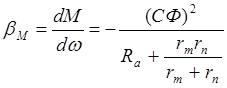                    (3.14)

выше жесткости характеристики:

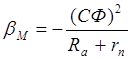                        (3.15)

для схемы с добавочным сопротивлением, но ниже жесткости:

                           (3.16)

естественной характеристики (рис.3.16).

Расчет сопротивлений, обеспечивающих работу двигателя со скоростью w_с<w_н при нагрузке на валу, равной М_с, производится следующим образом. 

Из (3.14) следует, что наибольшая жесткость механической характеристики обеспечивается при минимальном значении R_a+r_mr_n/(r_m+r_n). Минимальное значение равно. Тогда в соответствии с (3.12)

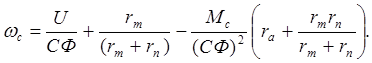           (3.17)

Введем обозначение a=r_n/r_m и решим уравнение (3.17) относительно a:

                  (3.18)

Из схемы (рис.3.7) и уравнения (3.18), которое принимает вид

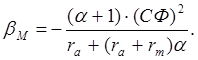                      (3.19)

следует, что наибольшему значению жесткости следует наименьшее значение a. В тоже время желательно иметь небольшие значения r_ш. Однако, протекающий через сопротивления r_m и r_п ток не должен быть чрезмерно большим. В режиме идеального холостого хода этот ток равен:

I_m=I_n=I₀=U/(r_m+r_n)=U/r_m(1+a).               (3.20)

Выражая r_m из (3.15) преобразуем (3.17) к виду:

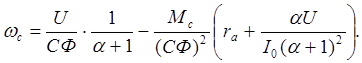            (3.21)

тогда

              (3.22)

где

A=r_aI₀M_c+w_c(CФ)²,

B=U(M_c-I₀CФ),

C=-I₀UCФ.

Очевидно, что значение a должно быть не комплексным. Этому условию удовлетворяет неравенство

(В-2А)²-4А(А-С)=В²-2А(В-2С)>0.

Так как

В-2С=UM_c-UI₀СФ+2UI₀CФ>0,

то подкоренное выражение в (3.22) может быть и положительным, и отрицательным в зависимости от значения I₀.

Теперь можно предположить следующий порядок расчета сопротивлений:

·  Для ряда значений I₀<I_н рассчитать a;

·  Из всех значений a выбрать наименьшее положительное значение;

·  Определить r_ш=U/(a+1), r_п=ar_ш.

3.6  Регулирование скорости двигателя постоянного тока с последовательным возбуждением изменением напряжения.

Из-за ухудшения условий коммутации при превышении напряжения на якоре по отношению к номинальному напряжение регулирование напряжения выше номинального не рекомендуется. При U=0 нет условий для возбуждения двигателя. Следовательно, напряжение можно регулировать при выполнении условия 0<U<U_н.

При снижении напряжения одновременно снижается и скорость вращения двигателя (при заданном моменте сопротивления) и жесткость характеристик. Рассмотрим этот вопрос подробно.

При заданном моменте сопротивления М_с и заданном напряжении устанавливается некоторая скорость вращения w_с. В соответствии с уравнением механической характеристики

Следовательно, значение потока, которое может при этом создаваться, можно получить как результат решения квадратного уравнения:

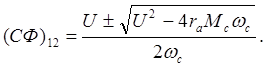
Проанализируем электромеханическую характеристику при

                 (3.23)

Так как в соответствии с уравнением электромеханической характеристики ток, который может установиться в якорной цепи, определяется уравнением

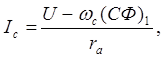
после подстановки находим:

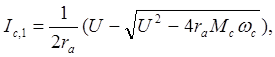                (3.24)

Для второго решения

                 (3.25)

получим

                (3.26)

Очевидно, что правильным является только решение (3.24). действительно, при М_с=0 должно выполняться условие: I_c=0. этому условию удовлетворяет лишь (3.24).

Отклонение скорости Dwc=r_aI_c,1/(CФ)₁ определяется следующим образом: