Второй закон термодинамики и понятие об энтропии были введены в физику первоначально при рассмотрении наиболее простого вида систем – систем изолированных, т.е. лишенных обмена энергией или веществом с окружающей средой. Только для таких систем направление самопроизвольного течения процессов и условия равновесия могли быть выражены однозначно через изменение энтропии S. Однако на практике большей частью приходится иметь дело с системой взаимодействующей с окружающей средой. Энтропия мало подходит для характеристики процессов в этих условиях.
В конце прошлого века в результате работ Гиббса, Массье, Гельмгольца и других были открыты термодинамические функции, изменения которых при тех или иных условиях существования системы давали возможность в простой форме определить направление самопроизвольного течения процесса и условия равновесия.
Характеристической функцией называется такая функция состояния системы, посредством которой или её производных могут быть выражены в явной форме термодинамические свойства системы.
Работа равновесного термодинамического процесса может быть рассчитана из следующего выражения:
![]() (1)
(1)
d – полный дифференциал;
d - бесконечно малое изменение этой величины.
Отсюда:
![]() (2)
(2)
где Q – теплота; А – работа; U – внутренняя энергия системы.
dА – для работы расширения по бесконечно малому объему:
![]() (3)
(3)
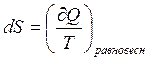
![]() (4)
(4)
Если подставить (3) и (4) в (2), то
![]() (5)
(5)
Термодинамическая система при стремлении к равновесию высвобождает часть внутренней энергии, передавая её в окружающую среду в виде теплоты или работы, эта составляющая внутренней энергии представляемая окружающей среде называется свободной энергией – G.
Свободная энергия имеет две составляющие тепловую и потенциальную. Взаимосвязь этих составляющих свободной энергии лежит в основе ряда физических явлений и превращений.
Свободная энергия является функцией состояния системы, поэтому её изменение зависит только от разности начальных и конечных состояний системы и не зависит от пути перехода из одного состояния в другое.
![]() , где Р – давление;
, где Р – давление;
Т – температура;
V – объем;
Sn – площадь поверхности системы;
С – концентрация компонентов;
Се – концентрация электрического заряда;
Е – напряженность электрического поля;
Hm – напряженность магнитного поля;
g – гравитационный потенциал.
Для удобства обозначим:
![]()
dG – функция от параметров состояния системы. Если параметры состояния термодинамической системы известны, то её можно описать следующим уравнением:
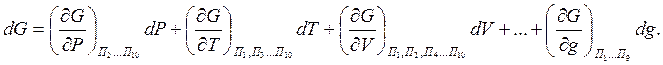 (6)
(6)
Пусть в систему входит к – компонентов, тогда концентрация:
![]()
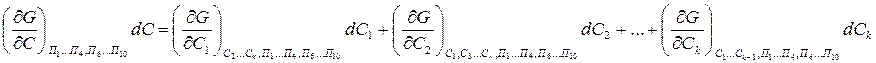
Частные производные от свободной энергии G по параметрам системы входящим в уравнение (6) имеют определенный физический смысл:
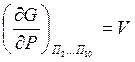 -объем системы;
-объем системы;
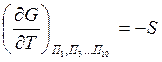 -
энтропия системы;
-
энтропия системы;
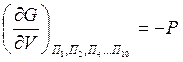 -
давление системы;
-
давление системы;
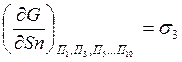 -
энергия поверхностного натяжения;
-
энергия поверхностного натяжения;
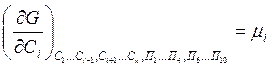 -
химический потенциал i –го компонента;
-
химический потенциал i –го компонента;
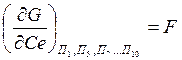 -
энергия Ферми;
-
энергия Ферми;
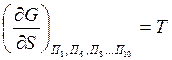 -
температура;
-
температура;
и т.д.
![]() -
параметрические потенциалы системы.
-
параметрические потенциалы системы.
Если для конкретной термодинамической системы некоторые параметры системы неважные, то уравнение (6) можно упростить. В отсутствии электрических, магнитных и гравитационных полей уравнение (6) можно записать:
![]() (8)
(8)
Часть свободной энергии системы G, которая может превращаться в работу расширения,
обозначается ![]() и рассчитывается:
и рассчитывается:
![]() (9)
(9)
![]() - свободная энергия Гельмгольца
(изохорный потенциал).
- свободная энергия Гельмгольца
(изохорный потенциал).
Если имеют место другие виды работы, кроме работы расширения, то функцию состояния можно записать следующим образом:
![]() (10)
(10)
![]() -
свободная энергия Гиббса (изобарный потенциал).
-
свободная энергия Гиббса (изобарный потенциал).
Энтальпия Н – это функция состояния системы, численно равная количеству теплоты выделяемой или поглощаемой системой в данном процессе:
![]() (11)
(11)
Связь между свободной энергией
Гельмгольца ![]() и внутренней энергией системы определяется
уравнением:
и внутренней энергией системы определяется
уравнением:
![]() (12)
(12)
Связь между свободной энергией Гиббса и этальпией определяется:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.