Физико-химические основы технологии электронных средств. Конспект лекций, страница 3

Из первого закона термодинамики нельзя определить возможность протекания процесса и его направление, что важно в конкретных случаях науки и техники.

Все процессы делятся на равновесные и неравновесные:

Равновесные процессы-процессы для течения которых не требуются затраты работы извне и в результате которых не может быть получена работа против внешних сил (передвижение шара по строго горизонтальной плоскости или качание маятника без трения).

Реальные процессы являются неравновесными.

Термодинамическая система, изменяясь, приближается к состоянию равновесия. С наступлением равновесия процесс заканчивается.

Существует два вида неравновесных процессов:

1.  Неравновесные процессы, которые идут в направлении равновесия без воздействия внешней силы.

2.  Обратные процессы, которые удаляют систему от состояния равновесия, и не могут идти без внешнего воздействия.

Процессы первого вида называются самопроизвольными или «положительными», процессы второго вида несамопроизвольными или «отрицательными».

В изолированной системе идут только положительные процессы, так как внешние воздействия исключены.

Второй закон термодинамики дает возможность предсказать направление хода процесса.

Существует две формулировки второго закона термодинамики:

Постулат Клаузиуса: - единственным результатом любой совокупности процессов не может быть переход теплоты от менее нагретой системы к более нагретой. Процесс теплопроводности необратим.

Постулат Томпсона: - теплота наиболее холодного тела из участвующих в круговом процессе не может служить источником работы. Самопроизвольный процесс превращения работы в теплоту (путем трения) необратим.

Энтропия.

Второй закон термодинамики вводит новую функцию состояния системы энтропию - S.

Математическое выражение для энтропии можно записать следующим образом:

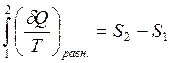
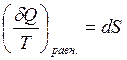
Энтропия – это функция состояния системы, изменение которой равно сумме приведенных теплот поглощенных системой в равновесном состоянии.

Это однозначная, непрерывная, конечная функция состояний.

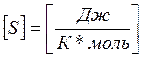 - энтропийная единица.

Рассчитав энтропию S можно предсказать направление процесса, если в  изолированной системе для какого-либо процесса энтропия S возрастает, процесс может идти самопроизвольно, если энтропия S уменьшается, то процесс невозможен. Если S=const, процесс равновесен, система бесконечно близка к состоянию равновесия.

Для неизолированной системы, обменивающейся с окружающей средой теплотой и работой, возможны процессы, сопровождающиеся как увеличением, так и уменьшением S.

Для того чтобы решить однозначно вопрос о направлении процесса в неизолированной системе, необходимо включить в систему все тела участвующие в процессе, сделав систему изолированной.

Условие изолированной системы можно записать так: U=const, V=const.

Признак равновесия изолированной системы заключается в том, что изолированная система находится в состоянии равновесия, если S – системы имеет максимальное значение (S=Smax) при U=const, V=const.

Математически условие S=Smax записывается так:

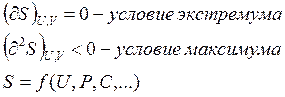
Третий закон термодинамики дает возможность вычислить абсолютное значение энтропии системы, с помощью постулата Планка:

Энтропия индивидуального идеального кристаллического вещества при абсолютном нуле равна нулю.

Для реальных кристаллов энтропия . Это подтверждено расчетами статистической термодинамики. Это выражение справедливо и для температуры абсолютного нуля, поэтому для реальных кристаллов .

Для идеального твердого тела:

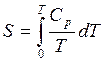       (1)

 где - теплоемкость данного вещества при постоянном давлении (P=const);

 T- температура.

Для большинства реальных кристаллических веществ: ~.

При Т®0 ®0 то есть .

Было замечено, что при Т®0 к нулю стремиться не только S и , но и объем тела и давление насыщенного пара изменяются с температурой так, что их производные по температуре стремятся к нулю.

Ни какие процессы не могут снизить температуру тела до абсолютного нуля – это принцип недостижимости абсолютного нуля.