Физико-химические основы технологии электронных средств. Конспект лекций, страница 7

Статистической природой обладают такие  величины, как плотность, удельный или мольный объем и.т.д.

Системы, состоящие из очень большого числа частиц, мы не можем в настоящее время описывать на основе обычных законов механики. Но, применяя теорию вероятности, законы которой в сочетании с законами механики образуют статистическую механику, можно определить большую или меньшую вероятность данного состояния системы. Системы с большим числом частиц достаточно строго описываются законами вероятности, и отклонения настолько маловероятны, что практически их можно считать невозможными.

Второй закон термодинамики с этой точки зрения устанавливает критерий большей или меньшей вероятности сравниваемых состояний и то, что в системе, состоящей из большого числа частиц, самопроизвольно могут происходить переходы только из состояния менее вероятного в состояние более вероятное.

Так возможность самопроизвольного перехода теплоты от более горячего тела к более холодному и невозможность самопроизвольного течения процесса в обратном направлении объясняется так:

Если в системе из двух тел с разной температурой, частицы, обладающие в среднем большей кинетической энергией в одной части, то через некоторое время за счет беспорядочного соударения частиц установится равномерное распределения средней кинетической энергией, что будет отвечать выравниванию температуры.

Процесс обратный соответствовал бы тому, что молекулы с большей кинетической энергией («более горячие») должны были бы сгруппироваться в одной части системы, а «более холодные» в другой, что, очевидно, является процессом совершенно невероятным, т.е. практически невозможным. При малом же числе частиц таких выводов сделать нельзя.

Макроскопическое состояние, характеризуемое определенными термодинамическими параметрами, может существовать при различном распределении молекул, т.е. оно осуществляется разными микросостояниями отличающимся друг от друга по определенному признаку. Вероятность каждого макросостояния пропорционально числу микросостояний, которыми оно осуществляется. Это число называется термодинамической вероятностью, этой величиной в статистической физике пользуются как мерой вероятности состояний.

Чтобы от термодинамической вероятности перейти к математической вероятности, необходимо значение термодинамической вероятности разделить на полное число всех возможных распределений молекул по данному признаку. Математическая вероятность всегда меньше единицы, а термодинамическая вероятность выражается большими числами.

Имеем систему, состоящую из двух частей. Всего N молекул, в одной части  - молекул, в другой (N-).

Термодинамическая вероятность: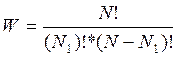  

Таким образом, второй закон термодинамики является не абсолютным законом, а статистическим, который соблюдается с высокой степенью точности для большого количества молекул, и тем меньше применим, чем меньше размеры системы.

Статистический характер второго закона термодинамики установил Больцман, который установил связь между энтропией системы и вероятностью состояния системы.

Энтропия S и термодинамическая вероятность W возрастает при необратимых процессах приближающих систему к равновесию и принимает максимальное значение при равновесии системы.

S – аддитивна, т.е. ,

а W – мультипликативна, т.е. .

 т.к. ;и.т.д. то

Отсюда следует, что функция f является логарифмической, т.е. функция произведения равна сумме функций отдельных частей.

Результатом решения этого уравнения является уравнение Больцмана, устанавливающее связь между S и W:

Возьмем в рассмотрение термодинамическую систему представляющую идеальный кристалл, т.е. кристалл без дефектов структуры и рассмотрим при Т=0К.

Вероятность состояния такой системы при абсолютном нуле равна единице. При абсолютном нуле кристалл может быть осуществлен только одним распределением молекул, атомов, ионов. Все молекулы данного сорта неразличимы по своим энергиям и расположению и обмен местами различных, по какому – либо признаку молекул невозможен, тогда: если (Постулат Планка).