Концентрация ограничивается пределом растворимости примеси, которая зависит от температуры, от соотношения физической структуры, природы легирующего материала и диффузианта (размеры атомов, совпадения типов химической связи, тип кристаллической решетки). При некоторой температуре концентрация достигает максимума, и с дальнейшим ростом температуры будет падать.
Если проводится многократная диффузия, то для
последней диффузии выбирается материал с максимальной предельной
растворимостью. Поскольку ассортимент примесей ограничен, более трех
последовательных диффузии обеспечить не удается. Примеси вводимые путем
диффузии называют диффузантами. Источниками диффузантов являются
химические соединения, они могут быть твердыми (бром бор 3 ![]() , хлорокись фосфора
, хлорокись фосфора ![]() ,
три хлорид фосфора
,
три хлорид фосфора ![]() ), жидкими (борная кислота
), жидкими (борная кислота ![]() ), газовыми (фосфин
), газовыми (фосфин ![]() ,
хлорид бора
,
хлорид бора ![]() ).
).
Для технологической реализации легирования применяются диффузионные печи, метод открытой трубы. В зависимости от того, в каком агрегатном состоянии используемый диффузант, могут быть одно-зонные и двух зонные печи.
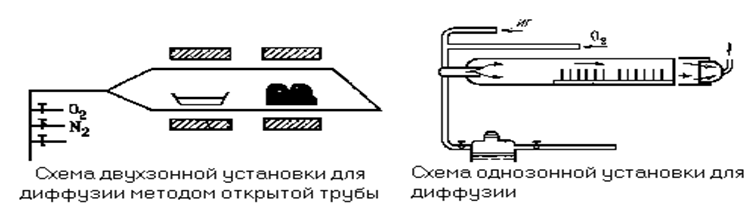
Если диффузант в твердом виде то применяется двухзонная печь, в неё запускается инертный газ (аргон) – первая зона печи служит для испарения диффузанта, а вторая для подогрева легируемых пластин, с целью ускорения процесса диффузии.
Если диффузант в жидком или газообразном виде, то используют одно-зонную печь. Сам диффузант располагается за пределами печи и его подают используя газ носитель.
Теория диффузии основана на двух законах Фика.
Первый закон связывает плотность тока и коэффициент диффузии 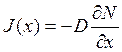 (1), второй закон характеризует накопление
примеси в некотором сечении легируемой пластины
(1), второй закон характеризует накопление
примеси в некотором сечении легируемой пластины 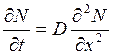 (2).
(2).
 Решение задачи сводится к
получению вида функции распределения примеси по глубине залегания и во времени N(x,t), для
этого необходимо решить второе уравнение Фика при заданных граничных условиях.
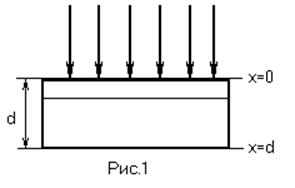
Первое граничное условие выводится из следующих соображений (рис.1). Толщина
легированного слоя значительно меньше толщины пластины d,
то есть N(d)=0 – на нижней
грани. С точки зрения математики d=¥ и тогда N(¥,t)=0 (3) – это
условие справедливо для всех типов диффузии.
Решение задачи сводится к
получению вида функции распределения примеси по глубине залегания и во времени N(x,t), для
этого необходимо решить второе уравнение Фика при заданных граничных условиях.
Первое граничное условие выводится из следующих соображений (рис.1). Толщина
легированного слоя значительно меньше толщины пластины d,
то есть N(d)=0 – на нижней
грани. С точки зрения математики d=¥ и тогда N(¥,t)=0 (3) – это
условие справедливо для всех типов диффузии.
Второе граничное условие имеет два варианта, которые соответствуют двум разновидностям реальных технологических процессов.
1. случай неограниченного источника примеси, в этом случае диффузант поступает непрерывно к поверхности пластины, так что в приповерхностном слое концентрация примеси поддерживается постоянной. Второе граничное условие имеет следующий вид N(0,t)=NS=const (4), где NS – поверхностная или приповерхностная концентрация примеси. Обычно количество поступаемого диффузанта обеспечивает режим предельной растворимости: NS=Nпр.max.
2. случай ограниченного источника, сначала в тонкий приповерхностный слой пластины вводят некоторое количество атомов диффузанта, потом отключают источник атомов диффузанта, затем нагревают пластину чтобы атомы примеси распределились по глубине пластины при неизменном их количестве: а) первая стадия – загонка примеси; б) вторая стадия – разгонка примеси.
Для того чтобы сохранить неизменным количество примеси в процессе разгонки необходимо обеспечить условие, при котором примесь будет распространяться только в глубь пластины, не испаряясь с её поверхности, поэтому до начала процесса разгонки поверхность пластины покрывают слоем металла, коэффициент диффузии примеси в которой значительно меньше коэффициента диффузии примеси в пластину.
Для варианта разгонки – второе граничное условие можно записать в следующем виде:
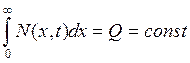 (5)
(5)
Q – количество атомов примеси на единицу площади поверхности задается на этапе загонки.
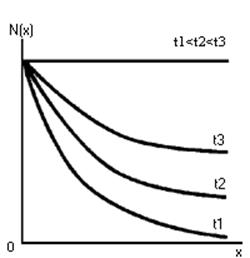 Решая (2) при граничных
условиях (3) и (4) получаем функцию распределения примеси по глубине залегания
и по времени:
Решая (2) при граничных
условиях (3) и (4) получаем функцию распределения примеси по глубине залегания
и по времени:
Для неограниченного источника:
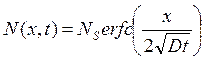 (6)
(6)
Решая (2) при граничных условиях (3) и (5) получаем функцию распределения:
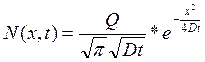 (7)
(7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.