Физико-химические основы технологии электронных средств. Конспект лекций, страница 4

Энтропия твердого тела определяется по выражению (1).

При плавлении и переходе в жидкую фазу энтропия возрастает на величину приведенной теплоты плавления:

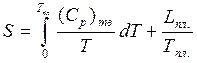     (2)

где - теплота плавления;

 - температура плавления.

Если нагреть жидкость от до температуры, то получим:

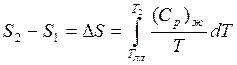  (3)

Энтропия пара может быть рассчитана:

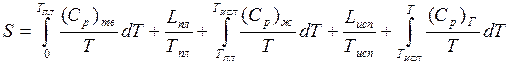   (4)

Для практических расчетов необходимо знать значение теплоемкости при постоянном давлении при температуре Т=10-80К, затем используют уравнение Дебая или Тарасова экстраполируют значение  к абсолютному нулю. По выражению (4) рассчитывается энтропия реального газа.

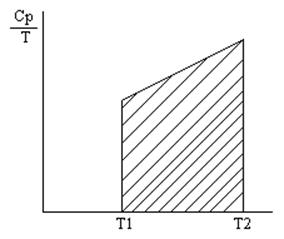
На практике интегральные выражения рассчитываются графически (см рис.) - численное значение интеграла определяют по площади заключенной между  и .

Энтропия зависит от молекулярного веса, агрегатного состояния (твердое®жидкое®газообразное энтропия возрастает), кристаллического строения (углерод, алмаз), от структуры молекул.

Условия равновесия термодинамических систем. Правило фаз.

Фазовые равновесия – это равновесия в системах, в которых не происходит химического взаимодействия между компонентами, а имеют место лишь фазовые переходы компонентов из одной фазы в другую.

Условие равновесия гетерогенной системы: во всех фазах гетерогенной термодинамической системы, Т и Р одинаковы и химические потенциалы m каждого из компонентов равны.

Химический потенциал – это величина, характеризующая способность компонента выделятся из данной фазы в рассматриваемых условиях.

Химический потенциал – это частная производная от энергии Ферми по концентрации данного компонента:

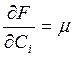
Одним из самых общих законов физической химии является закон равновесия фаз, называемый правилом фаз. Правило фаз основывается на втором законе термодинамики и относится к системам, находящимся в равновесии.

Возьмем систему, содержащую n – независимых компонентов и состоящую из k – фаз, находящихся в устойчивом равновесии между собой.

Составим уравнения выражающие условия равновесия для наиболее общего случая, когда все компоненты входят во все фазы, из которых состоит гетерогенная система:

n – число компонентов  (1…n),

к – число фаз (1…к)

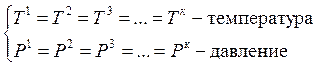      (1)

Выражение (1) ряды тождеств, т.к. Т и Р независимые переменные.

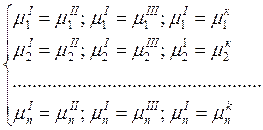    (2)

Выражение (2) это не ряды тождеств, т.к. химический потенциал одного компонента в различных фазах описывается различными функциями от Р, С, Т.

На основании (2) можно составить систему независимых уравнений.

Вид функциименяется от одной фазы к другой и в общем случае  неизвестен, каждое из равенств  является независимым уравнением.

Общее количество уравнений составляющих систему будет равно:

Т, Р, С – независимые переменные входящие в систему независимых уравнений.

Для выражения состава любой фазы, содержащей n – компонентов, достаточно указать процентное содержание (n-1) компонентов. Следовательно для описания состава всех к – фаз нам может потребоваться к*(n-1) данных и для полного описания еще Т и Р т.е. всего к*(n-1)+2 данных.

Если число независимых переменных равно числу уравнений их связывающих, то каждая переменная принимает некоторое, строго определенное значение и вся система может существовать при этом единственно возможном сочетании Т, Р и С во всех фазах, если же число уравнений меньше числа независимых переменных то разность (f) – это число переменных которым можно придавать произвольные значения при имеющихся уравнениях, а следовательно при данном числе фаз:

         (3)

f – число термодинамических степеней свободы системы, или вариантность системы определяется как число условий ( температура, давление, концентрации), которые можно произвольно менять ( в известных пределах ), не изменяя этим числа или вида фаз системы.

Если  f=1, то система моновариантная.

Если f=2, то система бивариантная.

Если f=0, то система нонвариантна.

Преобразуя (3) можно получить:

         (4)