Теория функций комплексного переменного. Поле комплексных чисел, страница 9

И2. [аддитивность] Если функция f(z) интегрируема по сумме кривых L₁+L₂, то она интегрируема по каждой кривой и

ò_{L_1+L_2} f(z) dz=ò_{L_1} f(z) dz+ò_{L_2} f(z) dz.    

И3 [изменение знака]  Если функция f(z) интегрируема по кривой L, то она интегрируема по противоположной кривой и

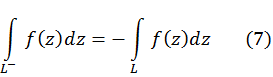
И4. Интеграл по точке равен нулю

14.3  Длина кривой

Длиной непрерывной кривой  L:  z=z(t), a ≤  t≤  b  называется предел интегральных сумм при . В курсе анализа действительной переменной доказывается, что длина кусочно-гладкой кривой существует (т. е. такая кривая  спрямляема) и длина выражается следующим интегралом:

Кроме этого длина обладает свойством аддитивности

что следует из аддитивности интеграла (8).

Вычислим длину единичной окружности:

.

Итак:  число "пи" равно половине длины единичной окружности.  Это есть геометрический смысл числа "пи".

И4[оценка интеграла]  Пусть |f(z(t))| ≤  M для любого t∈ [a , b ] спрямляемой кривой L. Тогда |ò _Lf(z) dz| ≤  M⋅  длина (L).

Вычислим интегралыОшибка! Источник ссылки не найден.   (n∈ℤ ) , которые позже понадобятся для представления  функции  в виде суммы ряда.

Если n=1, то этот интеграл равен 2πi, иначе он равен нулю. Итак:

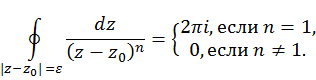
Как следствие получаем:  если γ_k -- окружность |z-z₀|=𝜺 , проходимая против часовой стрелки k раз, то ∮_{γ _k} dz/(z-z₀) =2πki .

15  Теорема Коши

15.1  Теорема Коши для односвязной области

Пусть функция f(z)=u(x,y)+iv(x,y) аналитична на замкнутой ограниченной многосвязной области D, и L -- замкнутая кусочно-гладкая кривая. Преобразуя интеграл ∮_L u dx-v dy по формуле Грина к двойному интегралу и учитывая условия Коши--Римана, получаем, что значение этого интеграла равно нулю. Аналогично доказывается равенство ∮_L udy+vdx=0. Итак:

Теорема Коши. Интеграл по замкнутому контуру от аналитической функции в односвязной области равен 0 .

Теорема. Пусть  аналитична в открытой ограниченной односвязной области D и непрерывна на ее замыкании. Тогда интеграл по границе этой области равен 0

Теорема. Пусть  аналитична в некоторой односвязной области G. Тогда интеграл   по всякой дуге, находящейся внутри области G зависит только от положения начальной и конечной точки и является аналитической  функцией. При этом

Доказательство. Заметим, что действительнозначная функция двух переменных  Φ (x,y)=ò^(x,y) u dx-v dy -- потенциал векторного поля (u,-v), а функция Ψ (x,y)=ò_{(x_0,y_0)}^(x,y) v dx+u dy -- потенциал векторного поля (v,u). Тогда

∂ (Φ +iΨ )/ ∂x =u+iv,     ∂ (Φ +iΨ )/ ∂y =-v+iu, откуда и следует результат. Отсюда получаем формулу для функций комплексного переменного, аналогичную формуле Ньютона-Лейбница:

ò_{z_1}^z_2 f(z) dz=F(z₂)-F(z₁)=F(z)|_{z_1}^z_2 .

15.2  Распространение на многосвязные области

Теорема Коши для многосвязной области. Пусть   аналитична в многосвязной области D и непрерывна на ее замыкании, тогда интеграл по границе областиD равен 0:

∮_∂D f(z) dz=0.

Доказательство.  Разрезая, можно превратить многосвязную область  в односвязную. Так, например, на  рис.

                                                              

                                                                           

                                                 D

Рис. Разрезание многосвязной области

D -- двусвязная область, ограниченная двумя гладкими кривыми L₁ и L₂. Тем самым ∂D=L₁+L₂. Разрезая эту область по кривой γ, получаем односвязную область D\γ  с границей L₁+L₂+γ +γ^-. Интеграл от функции f(z) по этой границе равен 0 по предыдущей теореме Коши. Тогда

∮_∂D f(z) dz=∮_∂D f(z) dz+ò_γ f(z) dz+ò_{γ ^-} f(z) dz=∮_∂(D\γ) f(z) dz=0.

16  Интегральная формула Коши

Пусть f(z) непрерывна на замкнутой ограниченной  области D с границей L=∂D и интеграл от нее по любому замкнутому контуру равен нулю. Выберем точку a внутри области  и рассмотрим круг |z-a| ≤ ρ, целиком лежащий внутри области D. Обозначим через c_ρ  окружность |z-a| = ρ , проходимую один раз против часовой стрелки. Тогда по условию имеем: