Теория функций комплексного переменного. Поле комплексных чисел, страница 3

Поле комплексных чисел, пополненное элементом ∞, с определенными для него выше правилами, назовем  расширенной комплексной плоскостью.

Поместим комплексную плоскость ℂ  в трехмерное пространство  и рассмотрим в этом пространстве сферу Римана . Точку N(0,0,1) назовем северным полюсом, а точку S(0,0,-1) назовем южным полюсом. Построим  стереографическую проекцию сферы Римана на комплексную плоскость, т. е. отображение  ℂ  такое, что для любой точки P∈ ℜ , не совпадающей с северным полюсом, точки N, P и (P)∈ ℂ  лежат на одной прямой. Получаем биективное соответствие между точками сферы Римана с выброшенным северным полюсом и точками комплексной плоскости.

Предложение. Стереографическая проекция задается  формулами:

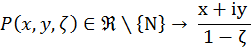
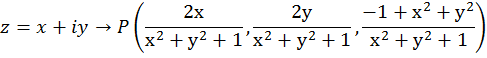Если последовательность точек P_n на сфере Римана стремится к N, то   и наоборот, если последовательность комплексных чисел  стремится к ∞ , то   приближается к северному полюсу по сфере Римана.

7  Дробно-линейная функция

7.1  Группа дробно-линейных преобразований сферы Римана

Функция вида  , где a,b,c,d∈ ℂ  и ad-bc≠ 0, называется  дробно-линейной . В частности, дробно-линейной функцией будет всякая  линейная функция  w=az+b с a≠ 0. Дробно-линейная функция неопределена в точке -d/c, но нетрудно вычислить, что предел функции    при  равен ∞. Полагаем по определению w(-d/c)=∞  и, кроме того, ясно, что w(∞ )=a/c. Тогда дробно-линейная функция задает биективное преобразование расширенной комплексной плоскости.

Предложение. Обратная к дробно-линейной функции   также будет дробно-линейной функцией  . Композиция дробно-линейных функций снова будет дробно линейной функцией.

7.2  Инверсия.

Для изучения свойств дробно-линейных преобразований понадобится понятие инверсии относительно окружности γ  радиуса R с центром в точке O. Точки P и P' называются  инверсными относительно γ, если они лежат на одном луче, выходящем из точки O,  и произведение расстояний от них до точки O равно R²:

OP⋅  OP'=R².          (1)

                                                                              A                                              P

 

                                                                      O         P’

Рис. 1 Инверсия относительно окружности

Преобразование евклидовой плоскости, переводящее всякую точку P, не совпадающую с O в инверсную точку P', называется  инверсией. При инверсии точки окружности γ  остаются неподвижными, внутренность круга OP'<R переходит во внешность этого круга и наоборот. Из определения инверсии вытекает геометрический способ построения инверсной точки P' по заданной точке P (рис. 1). Рассмотрим лишь случай, когда P лежит вне круга. Проводим касательную к окружности γ  из точки P. Пусть A -- точка касания. Опускаем перпендикуляр из точки A на луч OP. Инверсная точка P' будет основанием этого перпендикуляра.  Это следует из подобия треугольников OAP' и OAP:

OA / OP = OP'/OA, откуда R²=OA²=OP⋅OP'.

При инверсии центр круга переходит в бесконечно  удаленную точку. Наоборот, если P→ ∞ , то P'→  O. 

Предложение. Если евклидову плоскость превратить в плоскость комплексного переменного  так, что точка O изображает нулевое комплексное число, то инверсия будет задаваться формулой

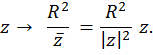
Действительно, числа z и R²/|z|²  z отличаются положительным множителем. Это показывает, что точки z и R²/ лежат на одном луче. Далее,

| z| ⋅ | R²/|z|² z|  =|z|⋅  R²⋅ |z|/|z|²  =R².

Предложение. Если на рис. 1 фиксировать точки P и M, а точку O устремить в бесконечность влево по горизонтальной прямой, то окружность γ  будет приближаться к перпендикуляру в точке M, а точка P'  будет стремиться к точке, симметричной P относительно этого перпендикуляра. Иными словами, симметрия относительно прямой есть предельный случай инверсии относительно окружности "бесконечно большого радиуса".□