Теория функций комплексного переменного. Поле комплексных чисел, страница 5

Имеют место обычные правила дифференцирования: производная суммы, произведения, частного и производная сложной функции. Производная постоянной функции равна 0. Если w=f(z) и z=g(w) -- две взаимно-обратные функции, то g'(w)= 1 / f'(z) .

Многочлен w=c₀+c₁z+… +c_nzⁿ является аналитической функцией на всей комплексной плоскости. Дробно-линейная функция   аналитична всюду, кроме точки -d/c (при c≠ 0), при этом ее производная w'= (ad-dc) /  (cz+d)²  нигде не обращается в ноль.

Пример. Функция  не аналитична ни в одной точке, так как отношение  стремиться к 1, если  и стремитькся к -1, если .

Предложение. Из аналитичности функции  следует ее непрерывность.

Условия Коши-Римана.  Если функция f(z)=u(x,y)+iv(x,y) аналитична в точке z₀, то выполнены условия

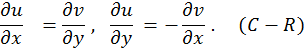
Наоборот, если в открытой области существут и непрерывны все четыре частные производные  и при этом выполнено в этой области условие (C-R), то функция  аналитична.

Доказательство.  Если f(z) аналитична, то рассмотрев два случая Δz=Δx и Δz=iΔy, получаем следующие значения производной: f'(z)=∂u/∂x+i∂v/∂x и f'(z)=-i∂u/∂y+∂v/∂y. Приравнивая действительные и мнимые части в равенстве ∂u/∂x+i∂v/∂x = -i∂u/∂y+∂v/∂y, получаем условия Коши-Римана.

Наоборот, если условия Коши-Римана выполнены и частные производные  непрерывны, то, учитывая дифференцируемость  функций u и v, выводим:

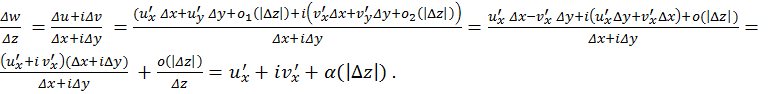для некоторой б.м. α . Устремляя Δz к нулю, получаем, что  производная w'_z существует и равна u'_x+iv'_x. □

9  Гармонические функции

Дифференциальный оператор Δ =∂²/∂x² + ∂² / ∂y²  называется  оператором Лапласа, а решения  дифференциального уравнения Лапласа  

∂²u / ∂x² + ∂²u/∂y² =0

называют  гармоническими функциями.  Например, все линейные функции  гармоничны.  Квадратичная форма  гармонична  тогда и только тогда, когда   т.е. .

Сформулируем две физические задачи, для которых математической моделью является уравнение Лапласа.

А. Пусть D -- физическая однородная пластинка, одинаковой толщины, теплоизолированная снизу и сверху. Обозначим через u(x,y) температуру в точке (x,y)∈  D. Полагаем, что температура на границе пластинки ∂D нам известна и поддерживается так, что она не зависит от времени. Тогда u(x,y) -- гармоническая функция, т. е. u(x,y) -- решение уравнения Лапласа с граничным условием, заданным распределением  температуры на границе пластинки.

Б. Пусть Γ  -- проволочный каркас, помещенный в пространство Oxyu так, что кривая Γ  есть график функции u(x,y), (x,y)∈  L, а L -- замкнутая гладкая кривая в плоскости Oxy (как, например, окружность), ограничивающая область D. Натянем на проволочный каркас мыльную пленку, и пусть функция u(x,y), (x,y)∈  D описывает вид этой мыльной пленки. Иными словами, мыльная пленка есть график функции u(x,y) с областью определения D. Тогда u(x,y) -- гармоническая функция.

Предложение. Если f(z)=u+iv -- аналитическая функция, то u и v -- гармонические функции.

Доказательство. Имеем:

∂²u/∂x² + ∂²u/∂y² =

Аналогично доказывается, что v -- гармоническая функция.

Более точно, функции u(x,y) и v(x,y) называются  сопряженными гармоническими функциями.

В полярных координатах оператор Лапласа имеет вид

10  Степенные ряды

Пусть

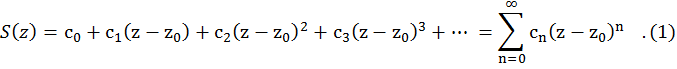
Через R обозначим радиус сходимости ряда (1). Тем самым ряд (1) равномерно сходится к  в любом круге  при условии . В частности  будет непреывной функцией на открытом круге .

Теорема. Функция S(z) аналитична в круге сходимости и

При этом ряд в правой части (2) имеет тот же радиус сходимости, что и ряд (1).

Далее будут рассматриваться также и ряды вида

Такие ряды заменой   сводятся к степенным рядам по степеням ζ . Из теоремы Абеля вытекает:

Следствие. Существует  неотрицательное действительное число r или +∞  такое, что ряд (3) сходится абсолютно в области |z-z₀| >r, и его сумма -- аналитическая в это

Пример.  Ряд - 1 / z – 1/  z^2 - 1 / z^3 -.... сходится в области | z| >1,  и его сумма совпадает в этой области  с функцией  .