Теория функций комплексного переменного. Поле комплексных чисел, страница 8

Если ψ : [a ', b ']→ [a, b ] -- непрерывное и биективное отображение, то функция z(ψ (s)), где s∈ [a ', b '] также задает путь L. Такая процедура называется заменой параметра. Заметим, что линейное отображение ψ (s)= (b-a )(s-a ')/(b ‘-a ‘)+a   биективно переводит отрезок [a ',b '] в отрезок [a ,b ]. Можно определить операцию сложения над дугами кривых. Описательно, сумма L₁+L₂ означает, что сначала проходим путь L₁, а потом путь L₂.

Для всякой дуги кривой L можно построить дугу L^-, проходимую вдоль L от конца до начала. Заметим, что дуги могут складываться и в случае, когда конец первой не совпадает с налом второй. Например, для кольца K:  граница , где   и  суть окружности, проходимые против часовой стрелки. Здесь граница  -- кусочно гладкая кривая, состоящая из двух гладких кусков.

Окружность радиуса ρ  с центром  в точке z₀, проходимая один раз против часовой стрелки, задается так: z(t)=z₀+ρe^it  и 0≤  t≤  2π . Это гладкий непрерывный замкнутый путь. Обозначим его c_ρ (z₀). Путь c_ρ (z₀)+… +c_ρ (z₀) (k раз), т. е.  есть  k раз проходимая окружность; она задается той же функцией, но t∈ [0, 2πk]. Граница квадрата 0≤  x≤ 1, 0≤  y≤  1 -- сумма отрезков L₁+L₂+L₃+L₄, где

L₁:z(t)=t;     L₂:z(t)=1+it;     L₃:z(t)=1-t+i;     L₄:z(t)=i(1-t);

и параметр t меняется всюду от 0 до 1. Граница квадрата -- замкнутый, непрерывный и кусочно-гладкий,  но не гладкий путь.

Граница области всегда проходится так, что область остается слева. Это правило задает ориентацию границы.

Пусть  -- две непрерывных кривых, носители которых лежат в области  Скажем, что эти кривые гомотопны в области   если можно подыскать непрерывную функцию , что  и  тождественно по t.

Далее рассматриваются только области, у которых граница есть кусочно гладкий замкнутый путь, состоящий из конечного числа кусков

 

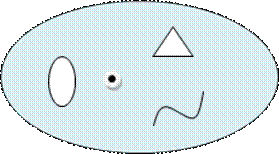Пример области, у которой граница состоит из пяти непрервных кусков

Область D называется  связной, если для любых ее точек z₁ и z₂ найдется непрерывный путь L, целиком лежащий в этой области и соединяющий точки z₁ и z₂.

Теорема. Следующие условия на связную область  эквивалентны:

а) граница  состоит из одной замкнутой кривой; б) любой непрерывный замкнутый путь, носитель которого лежит в  гомотопен в  точке;

в) любые два непрерывных пути с одинаковыми началами и концами. носителькоторых лежитв  гомотопны в

Такие области будем называть односвязными. Область  назвем n-связной, если ее граница разбивается в дизъюнктное объединение  n непрерывных кусков. Примером связной, но не односвязной области является кольцо.

14.2  Определение и свойства интеграла

Пусть L: z=z(t), a ≤  t≤ b  --  непрерывная кривая. Рассмотрим  разбиение отрезка [a, b ] с отмеченными точками:

Обозначим Δz_j=z(t_j)-z(t_j-1 ). Параметром разбиения  назовем неотрицательное действительное число

Предположим, что нам задана функция f(z), определенная на множестве, содержащем носитель кривой L. Составим  интегральную сумму:

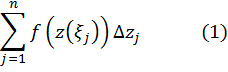
Интегралом функции f(z) по  кривой L  называется предел интегральных сумм (1), если параметр разбиения стремится к 0:

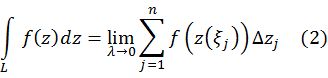
Если кривая  не является непрерывной, но есть сумма непрерыных кривых  , носители которых не пересекаются, то по определению

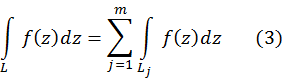
Теорема. Если  – кусочно-гладкая кривая, а  кусочно-непрерывная на носителе , то интеграл (2) существует, причем

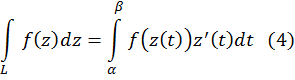
Доказательство. Обозначим ,  ,   (1≤ j≤ n). Тогда

Переходя здесь к пределу , получим, что правая часть (5) имеет предел раный сумме двух криволинейных интегралов. Тогда

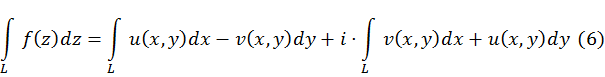
Для гладкой кривой  формула (6) дает возможность сведения к определенному интегралу по отрезку (см. (4)) □  

Сформулируем без доказательства стандартные свойства интеграла.

И1. [линейность]  Для любых a,b∈ ℂ  и любых функций f(z), g(z), интегрируемых по кривой L, имеет место равенство:

ò_L(af(z)+bg(z)) dz=a ò_Lf(z)dz+b ò_L g(z) dz.