Теория функций комплексного переменного. Поле комплексных чисел, страница 4

Теорема (геометрическая характеристика дробно-линейных преобразований).

1.  Преобразование  есть поворот на угол  относительно 0.

2. Преобразование , где  есть гомотетия с центром 0.

3. Преобразование  есть параллельный перенос на «вектор»

3. Преобразование  есть композиция инверсии относительно единичной окружности и отражения относительно действительной оси.

4. Любое дробно-линейное преобразование можно представить в виде композиции преобразований, указанных выше.

Доказательство. Заметим, что

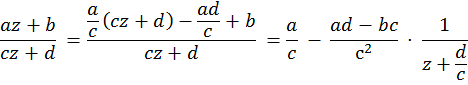
в том случае когда c≠ 0, т. е. в том случае, когда дробно-линейное преобразование не является линейным. Согласно определению дробно-линейного преобразования, число ad-bc  не нулевое. Любое ненулевое комплексное число можно представить  в виде произведения r⋅a, где |a| =1 и r∈ ℝ^>0 . □

Под  окружностью в расширенном смысле  будем понимать либо окружность в привычном смысле, либо прямую как окружность бесконечного радиуса. Уравнение такой окружности будет

A(x²+y²)+Bx+Cy+D=0, где A,B,C,D∈ ℝ  и первые три коэффициента не равны одновременно нулю. Случай A=0 соответствует прямой. Заметим, что это уравнение можно переписать в виде  

где A,D∈  ℝ  и M=B/2+C/(2i)∈ ℂ .

Теорема [круговое свойство] Всякая дробно-линейная функция переводит окружность в расширенном смысле в окружность в расширенном смысле.

Доказательство.  В виду предыдущей теоремы  и того элементарного факта, что параллельный перенос, поворот, гомотетия и симметрия переводят окружность в окружность, а прямую в прямую, доказательство достаточно провести для преобразования вида  w= 1/z . Пусть (2) -- уравнение окружности в расширенном смысле. Тогда z=1 / w  и уравнение ( 2 ) переписывается так:

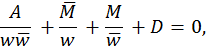
или

Это уравнение также задает окружность в расширенном смысле на плоскости w (при D=0 получаем прямую).□

Предложение 1. Дробно-линейная функция, отображающая верхнюю полуплоскость на внутренность единичного круга имеет вид

Предложение 2. При любом дейсвительном   и любом комплексном α, не принадлежащем единичной окружности, дробно-линейная функция следующего вида:

отображает  единичную окружность на себя. Если , то (3) отображает единичный круг на себя, а при  (3) отображает единичный круг на внешность единичного круга.  

Доказательство.  Во-первых  в силу того, что α ∉ 𝕊 . Далее:

| w(1)| =|1-α |/|1-\ov a|  =| 1-α |/ |\ov( 1- α )|   =1,

| w(-1)| =| -1-α |/|1+\ov α |  =|1+α |/ |\ov( 1+ α )|   =1,

|w(i)| =| i-α |/|1-i\ov α |  = | i-α |/|(-i-\ov α  )i|  =| i-α |/|\ov (i-α)|    =1.

Итак: w(1), w(-1), w(i) -- три различные точки, лежащие на единичной окружности. Следовательно, w(𝕊 )=𝕊 в силу кругового свойства. Так как w(0)=a⋅ α  и | w(0)| =|α | , то при |α | >1  единичный круг отображается на внешность единичного круга, а при  |α | <1 дробно-линейное преобразование (3 ) отображает единичный круг на себя.□

Предложение 3. Группа дробно-линейных преобразований, оставляющих верхнюю полуплоскось на месте, состоит из функций вида

Доказательство. Так как  , то . Умножая числитель и знаменатель дроби на , если  или на  если  (и тогда обязательно  ), сводим доказательство к случаю, когда . Так как , то    для некоторого . Кроме того,  и поэтому  для действительного t.   Подставляя второе соотношение в первое, получим,

Заметим, что , иначе  и  -- противоречие с определением дробно-линейного преобразования. Тогда из (4) вытекает, что , а значит и  -- действительны.

Обратное утверждение очевидно.□

8  Аналитичность

Пусть функция f(z) определена в окрестности точки z₀.  Производная функции комплексного переменного w=f(z) в точке z₀  определяется в точности также как и для функции действительного переменного.

Функция комплексного переменного называется  аналитической в точке, если она имеет производную в некоторой окрестности этой точки.  Аналитичность на замкнутой области D  означает существование производной на некоторой открытой области G, содержащей D.