ò _|z| =3 dz/ z^3-5z^2+4z =2\pi i[\Res(\frac 1 z^3-5z^2+4z ,0)+
\Res(\frac 1 z^3-5z^2+4z ,1)]= = 2\pi i[\frac 1 z^2-5z+4 left/_ z=0 +
\frac 1 z(z-4) /_ z=1 .]=2\pi i(\frac 1 4 -\frac 1 3 )=-\frac \pi i 6 .
Предложение. Предположим, что бесконечно удаленная точка является нулем второго или более высокого порядка функции f(z), т.е. разложение в ряд Лорана в окрестности ∞ имеет вид
f(z)=c_ -2 / z^2 + c_ -3 / z^3 + c_ -4 / z^4 +...
Допустим также, что f(z) является аналитической функцией на действительной оси, а в верхней полуплоскости Im z>0 имеет лишь конечное число особых точек a_1,a_2,...,a_n. Тогда
ò _ -∞ ^ +∞ f(x) dx=2πi∑ _ j=1 ^ j=n Res[f(z),a_j] (1)
Доказательство. Все лежащие в верхней полуплоскости особые точки можно заключить внутрь расположенного в верхней полуплоскости полукруга достаточно большого радиуса R с центром в начале координат. По основной теореме о вычетах получаем
ò _L f(z) dz+ò _ -R ^ +R f(x) dx=2πi∑_ j=1 ^n Res[f(z),a_j], (2)
где L -- верхняя полуокружность радиуса R, проходимая против часовой стрелки. Так как f(z)=g(z)/z^2 , где g(z) -- ограничена на бесконечности, например, числом M, то
|ò _L f(z) dz |=|ò _L g(z)dz / z^2| ≤ M / R^2 ⋅ π R=M/πR → 0
при R→ +∞ . Тогда, переходя в соотношении (2) к пределу R→ +∞ , получаем требуемое равенство.
Пример. Вычислим интеграл:
ò_ -∞^ +∞ dx / (x^2+1)^2 =2πi Res[1/(z^2+1)^2 ,i]=2πi(-1/4i)= π/2 .
Лемма К. Жордана (лЖ). Пусть на
некоторой последовательности дуг окружностей ![]() (
(![]() – фиксировано) функция
– фиксировано) функция ![]() стремится к нулю равномерно относительно
стремится к нулю равномерно относительно ![]() Тогда для любого положительного числа λ
Тогда для любого положительного числа λ
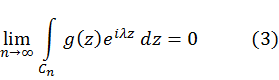
![]() Доказательство. Обозначим
Доказательство. Обозначим ![]() . По условию леммы
. По условию леммы ![]() при
при ![]() . Величина
. Величина ![]() также стремится к 0, причем
также стремится к 0, причем ![]() . Пусть сначала a>0.
. Пусть сначала a>0.
 E
На рис.
E
На рис. ![]() . На дугах АВ и CD имеем
. На дугах АВ и CD имеем
![]()
![]()
![]() C B
C B
![]() , следовательно
, следовательно ![]()
D -a A ![]() . На основании неравенства
. На основании неравенства
Рис. Лемма Жордана ![]() , справедливого при
, справедливого при ![]() , мы
заключаем, что на дуге BE имеет место неравенство
, мы
заключаем, что на дуге BE имеет место неравенство
![]()
Следовательно,
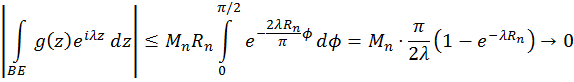
Если для дуги EC отсчитывать
полярный угол от отрицательной полуоси, то оценка интеграла по этой дуге будет
такая же как и для дуги BE. Случай ![]() разобран.
Случай
разобран.
Случай ![]() еще проще – не надо оценивать интегралы по
дугам AB и CD. □
еще проще – не надо оценивать интегралы по
дугам AB и CD. □
Замечание. Последовательность дуг ![]() можно заменить на семейство дуг
можно заменить на семейство дуг ![]() радиуса
радиуса ![]() .
.
Переформулировка леммы Жордана. Заменим ![]() . Пусть
на некотором семействе дуг окружностей
. Пусть
на некотором семействе дуг окружностей ![]() радиуса
радиуса ![]() и
и ![]() функция
функция ![]() стремится к нулю равномерно относительно
стремится к нулю равномерно относительно ![]() Тогда для любого положительного числа t
Тогда для любого положительного числа t
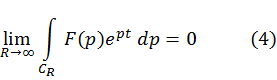
Следствие. Пусть f(z)=e^ imz F(z), причем m>0, и F(z)→ 0, когда z→ ∞ по любому закону, оставаясь, однако в области Im z≥ 0. Предположим, кроме того, что f(z) аналитична, а в верхней полуплоскости имеет не более конечного числа особых точек a_1,a_2,...,a_n. Тогда
ò _ -∞ ^ +∞ f(x) dx=2π i∑ _ j=1 ^ j=n Res[f(z),a_j].
Пример Вычислим интеграл:
ò _ -∞^ +∞ xcos x dx / x^2-2x+10 =ò_ -∞^ +∞ ze^ iz dz / z^2-2z+10 = = Re 2πi⋅ Res[ze^ iz/ z^2-2z+10 ,1+3i] =Re 2πi(1+3i)e^(-3+i)/2(1+3i)-2 = 3πe^(-3)(cos1-3sin1).
Интеграл Дирихле. Вычислим следующий интеграл: ò_0^ +∞ sin x/x dx. Он равен интегралу 1/2 Re ò_ -∞^ +∞ e^ ix /x dx . Имеем:
ò_ -∞^+∞ e^ ix / x dx=πi⋅ Res[e^ iz / z ,0]=πi.
Отсюда следует равенство:
ò_0^ +∞ sin x / x dx=π / 2 .
[БН] Бугров Я.С., Никольский С.М. Диффeренциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. -- М.: Наука, 1989. -- С.367-430.
[ЛЭ] Лунц Г.Л., Эльсгольц Л.Э. Функции комплексного переменного. -- СПб, 2002. -- 298с.
[ЛШ] Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. Гостехиздат, 1951 -- 496с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.