Теория функций комплексного переменного. Поле комплексных чисел, страница 6

11  Основные функции комплексной переменной

Напомним определение  комплексной экспоненты – . Тогда  

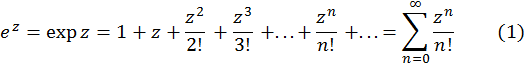
-- разложение в ряд Маклорена. Радиус сходимости этого ряда равен +∞, значит  комплексная экспонента  аналитична на всей комплексной плоскости и

(exp z)'=exp z; exp 0=1.     (2)

Первое равенство здесь следует, например,  из теоремы о почленном дифференцировании степенного ряда.

11.1  Тригонометрические и гиперболические  функции

Синусом комплексного переменного  называется функция

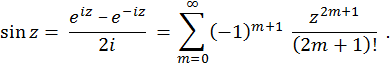
Косинус комплексного переменного  есть функция

Гиперболический синус комплексного переменного  определяется так:

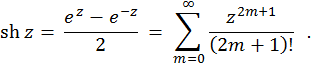
Гиперболический косинус комплексного переменного  --  это функция

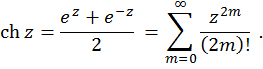
Отметим некоторые свойства вновь введеных функций.

A.  Если x∈ ℝ , то cos x, sin x, ch x, sh x∈ ℝ .

Б. Имеет место следующая связь тригонометрических и гиперболических функций:

cos iz=ch z;     sin iz=ish z,      ch iz=cos z;     sh iz=isin z.

В. Основные тригонометрическое и гиперболическое тождества:  

cos²z+sin²z=1;            ch²z-sh²z=1.

Доказательство основного гиперболического тождества.

Основное тригонометрическое тождество следует из оновного гиперболического тождества при учете связи тригонометрических и гиперболических функций (см. свойство Б)

Г  Формулы сложения:  

 

В частности,

Д. Для вычисления производных тригонометрических и гиперболических функций следует применить теорему о почленном дифференцировании степенного ряда. Получим:

(cos z)'=-sin z;     (sin z)'=cos z;     (ch z)'=sh z;     (sh z)'=ch z.

Е. Функции cos z, ch z четны, а функции sin z, sh z нечетны.

Ж. (Периодичность)   Функция e^z периодична с периодом 2π i. Функции cos z, sin z периодичны с периодом 2π , а функции ch z, sh z периодичны с периодом 2πi. Более того,

Применяя формулы суммы, получаем

З. Разложения на действительную и мнимую части:

Если однозначная аналитическая функция f(z) отображает биективно область D на область G, то D называется  областью однолистности.

И.  Область D_k={ x+iy | 2π k≤  y<2π (k+1)}  для любого целого k является областью однолистности функции e^z, которая отображает ее на область ℂ* .

Доказательство.  Из соотношения (5) следует инъективность отображения exp:D_k→ ℂ . Пусть w -- любое ненулевое комплексное число. Тогда, решая уравнения e^x=|w| и e^iy =w/|w| с действительными переменными x и y (y выбираем из полуинтеравала [2πk, 2π (k+1))), получим z=x+iy∈D_k такое, что exp z=w. Сюръективность доказана.

Следствием предыдущего свойства является

К. Область значений.  Область значений функций cos z, sin z, ch z, sh z есть все поле комплексных чисел.

Л.  Нули  Решением уравнения  sin z=0 является множество {πk | k∈  ℤ } . Нули функции cos z -- множество { π /2+πk | k∈  ℤ } . Нулями функции sh z является множество { πki | k∈  ℤ} , а нули функции ch z -- множество { π/2i+πki | k∈  ℤ } .

Доказательство.  Имеет место соотношения sin z=0 тогда и только тогда, когда e^iz -e^-iz =0 Это равносильно соотношению e^2iz =0, что дает 2iz=2πik. Окончательно,  z=2πk      (k∈ ℤ ). Аналогично доказываются утверждения для остальных функций.□

Функция tg z=sin z /cos z  называется  тангенсом, а функция th z= sh z/ ch z  называется  гиперболическим тангенсом. Производные тангенсов вычисляются c использованием известного правила "производная отношения":

(tg z)'=1/cos²z ,     (th z)'= 1/ch²z .

Область допустимых значений тангенса tg z есть многосвязная область ℂ \{π /2+πk | k∈ ℤ }

12  Аргумент комплексного числа

Главным значением аргумента ненулевого комплексного числа  z назовем то единственное действительное число 𝜑 ∈ [0,2π ), для которого  z /| z|  =exp(i𝜑 ). Обозначаем главное значение аргумента как arg z.

Всевозможные решения уравнения exp(i𝜑 )= z /| z|   относительно переменной 𝜑, т.е. множество {arg z+2π  k ∣  k∈ ℤ }  назовем  аргументом комплексного числа  z и обозначим Arg z. Таким образом Arg z -- многозначная функция.