Теория функций комплексного переменного. Поле комплексных чисел, страница 2

Умножая произвольное комплексное число-вектор  на комплексное число вида , увеличиваем аргумент у комплексного числа  на величину , не меняя модуля. Это преобразование соответствует повороту комплексной плоскости на угол  Умножение на положительное действительное число  есть гомотетия комплексной плоскости (растяжение в  раз, если  и сжатие в  раз, если ). Итак, преобразование

представляет из себя последовательное выполнение двух геометрических преобразований над вектором   -- поворота и гомотетии. В этом и заключается геометрический смысл умножения комплексных чисел.

Пример. Вычислим . Для этого сначала найдем модуль и аргумент числа :

Для того чтобы найти аргумент изобразим комплексное число  вектором, очевидно лежащем на биссектрисе первого квадранта, и ответ  или, по другому,   станет понятен. Далее

4  Комплексная экспонента

Правило (2) предыдущего параграфа дает нам право определить экспоненту чисто мнимого числа:

Действительно,  таким образом определенная функция   обладает следующими свойствами:

Здесь первое равенство есть частный случай (2) предыдущего параграфа, когда , второе равенство есть не что иное как формула Муавра, а третье равенство вытекает из периодичности гармоник. Заметим, что никакой коллизии в обозначения в связи с известной экспонентой  действительной переменной не возникает; равенство аргументов  возможно лишь если . Но тогда определение (1) комплексной экспоненты дает нам значение , что совпадает с известным равенством .

Определение (1) позволяет записать ненулевое комплексное число в показательной форме

В таком виде легче оперировать с комплексными числами, когда речь идет об умножении, делении и возведении в степень. Например,

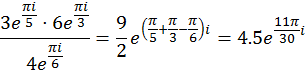
Определим теперь комплексную экспоненту для любого комплексного числа

Функция  будет уже функцией комплексного переменного. Для нее справедливы свойства

Е1. Область определения – все комплексные числа.

Е2.   ;

Е3.   —«школьная экспонента»

Е4. Комплексная экспонента периодична с периодом

Е5. Область значений – все комплексные числа, кроме нуля

4.1  Извлечение корней из комплексных чисел.

C помощью комплексной экспоненты легко извлекаются корни из комплексных чисел. Решим уравнение . Если w=0, то имеется только один нулевой корень кратности n. Пусть . Запишем  в показательном виде , где . Найдем арифметический корень n-ой степени из r  и обозначим его . Тогда уравнение  имеет n корней, расположенных на окружности радиуса  в вершинах правильного n-угольника

/*/ Действительно, применяя формулу Муавра, легко проверить, что все  -- корни уравнения  Пусть  – какой-либо корень уравнения . Тогда . Приравнивая модули, получаем равенство . Сокращая на  и деля на , получим  откуда  и . Это значит, что  для некоторго целого .   Поделим  на  с остатком: , где . Тогда

и . Следовательно, .

Корни (3) расположены в вершинах правильного - угольника, вписанного в окружность радиуса , имеющей центр в нулевой точке. 

Например, найдем корни уравнения . Здесь  арифметический корень шестой степени из 64 равен 2, а агрумент  равен нулю. Следовательно, корни имеют вид

5  Последовательности и ряды комплексных чисел

Предложение 1. Пусть – последовательность комплексных чисел, . Тогда

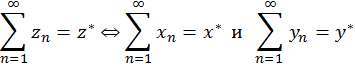
Доказательство вытекает из непрывности отображений  и  А именно, если  мало, то и  малы, а также если  малы, то   мал (модуль мал). □

Предложение 2.  Из абсолютной сходимости следует сходимость ряда.  

Докажем этот факт.  Обозначим . Тогда для любого 𝜺 >0 найдется, благодаря критерию Коши, натуральное N такое, что для любых  имеет место неравенство   Без ограничения общности можно считать, что . Тогда

Применяя снова критерий Коши к ряду , получаем его сходимость. □

6  Расширенная комплексная плоскость

Открытую область |z|>R  считаем R-окрестностью бесконечно удаленной точки ∞ . Считаем:

z/∞  = 0,     ∞ +z=z+∞ =∞     (z∈ ℂ ),      c/0 =∞ ,     ∞ ⋅  c=c⋅ ∞ =∞     (c∈ ℂ *).