Анализ простых облигаций, их доходность, форвардная ставка процента, страница 8

Первое слагаемое показывает доходность в результате изменений процентных ставок (случайная величина), второе - связанную с действием фактора времени, третье - влияние величины купонного процента, четвертое - "процента на процент" (случайная величина).

Поскольку первое слагаемое является случайной величиной, важно продолжить его анализ. Как следует из формулы (1.11),

[относительное изменение цен]=-D[относительное изменение (1+y)]

или

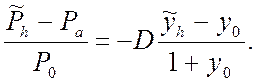
После несложных алгебраических преобразований получим:

	(1.19)
	(1.20)
где	(1.21)

Величина v показывает приблизительное изменение (P_h-P_a)/P_o на единицу изменения (y_h-y_o). Подставив в формулу (1.20) ожидаемую величину y_h, можно рассчитать ожидаемую доходность за период владения. При использовании различных величин y_h с учетом их вероятностей можно оценить вероятности различных значений R_h и, следовательно, величину риска для облигаций.

2.4. Планируемая доходность

Период владения N_h может быть меньше срока, который остается до погашения облигации. Цена, по которой инвестор планирует продать облигацию, зависит от ожидаемой инвестором рыночной ставки процента- Планируемую доходность можно рассчитать, решив относительно К уравнение:

(2.10)

Поскольку продажная цена Р_h в момент инвестирования неизвестна, желательно рассчитать планируемую доходность при различных продажных ценах Р_h.

Пример.

Облигация фирмы В может быть куплена за 850$. Срок погашения -15 лет. Купонная ставка 9 ½%. Облигацию планируется продать через 8 лет.

Решение:

где P₁ - текущая рыночная цена, К - доходность, N_h - период владения, P_h - цена в конце периода владения, С - купонная ставка.

.

Решая, получим К=13.34%.

2.5. Расчет продолжительности безрискового периода

Далее будет показано, что фактическая доходность ниже доходности к погашению, если проценты реинвестируются по ставке процента ниже доходности к погашению. Кроме того, облигация может быть продана до истечения срока погашения и тогда, если процентные ставки повысятся, цена облигации может быть достаточно низкой. Выделяют два типа риска, связанного с облигациями. Во-первых, это, реинвестиционный риск. Во-вторых, это риск, связанный с потерями о случае продажи облигации до истечения -срока погашения. Второй тип риска можно элиминировать путем покупки облигации со сроком погашения, равным периоду владения. Первый тип риска нельзя элиминировать таким путем. Падение процентных ставок приведет к снижению ставки реинвестирования, но, вместе с тем, повысит цену облигации. Таким образом, цена и ставка реинвестирования движутся в противоположных направлениях. Оба типа риска имеют место только, если период владения меньше срока погашения. Они могут в точности компенсировать друг друга. В этом случае говорят, что облигация имеет иммунитет, а период D при котором оба типа риска взаимно компенсируют друг друга называют иммунным (безрисковым). Предполагая, что проценты выплачиваются раз в полгода, иммунный период D можно рассчитать следующим образам:

(2.11)

В знаменателе формулы - текущая стоимость облигации, номинал которой равен 1000$. Денежные потоки в числителе взвешиваются по числу лет до погашения. Поскольку проценты выплачиваются раз в полгода, то весовые коэффициенты меняются от 0.5 до N.

Иммунный период можно рассчитать, используя эластичность цены облигации по доходности:

.

Можно показать, что

.

Зная эластичность облигации, можно рассчитать иммунный период и наоборот. Если инвестор владеет облигацией в течении иммунного периода, то доходность его инвестиций в эту облигацию равна доходности к погашению.