Анализ простых облигаций, их доходность, форвардная ставка процента, страница 6

Текущая стоимость каждой облигации определяется простым суммированием текущих оценок всех платежей. Облигация с трехпроцентным ("низким") купоном будет продаваться с дисконтом по цене 71.39 долларов, а облигация с десятипроцентным ("высоким") купоном с премией по цене 121.98 рубля. Хотя цены облигаций полностью обоснованы, они не обеспечивают одинаковой доходности (см.табл.1.10). Доходность по низкокупонным облигациям превышает тот же показатель по высококупонным облигациям на 20 базисных пунктов.

Приведенный пример иллюстрирует общий вывод: в условиях роста будущих ставок низкокупонные облигации обеспечивают более высокую доходность, а в условиях снижения будущих процентных ставок более выгодны высококупонные облигации.

Доходность бескупонных облигаций (y) - это средняя всех будущих ставок до срока её погашения, т.е.

где  f_t - будущая ставка для t-го года.

Если будущие ставки растут (падают), то доходность дисконтных облигаций (бескупонных) будет меньше (больше) соответствующих будущих ставок. Доходность по купонным облигациям будет меньше (больше) доходности дисконтных облигаций, если будущие ставки растут (падают).

1.5.6. Премия за возможность неплатежа и риск

Обыкновенные акции не связаны с гарантиями каких-то платежей. Для них должны быть рассмотрены все возможные результаты и соответствующие вероятности. Ожидаемая доходность по акциям равна средневзвешанной всех возможных исходов, причем в качестве весов используются вероятности.

Подобная методика применима и для облигаций. Если имеется возможность неплатежа, то ожидаемая доходность может быть ниже обещанной (максимальной). Чем больше риск неплатежа и сумма связанных с этим убытков, тем больше будет разница между этими величинами.

Ожидаемую доходность полезно сравнить с доходностью по безрисковым инструментам. Для акций в качестве этих инструментов принимают казначейские векселя, для облигаций - это безрисковые облигации с примерно равным сроком погашения. Разница в доходности между ними образует премию за риск.

Величина премии за возможность неплатежа зависит как от вероятности его, так и от возможных убытков в случае неплатежа.

Предположим, вероятность неплатежа по данной облигации одинакова для каждого года и равна p_d. В случае, если эта возможность реализуется, по облигации выплачивается сумма, равная определенной доле цены за год до погашения облигации (λ). Максимальная доходность для такой облигации (y) равна (вывод формулы опущен):

где r - ожидаемая доходность облигации.

Разность между y и r равна премии за возможность неплатежа (d):

Пример. За период 1929-1939 гг. в среднем за год в США было отмечено по 2.3% случаев неплатежей от всех выпущенных облигаций среднего уровня. Владельцы этих облигаций получили лишь половину их номинальной стоимости (принимаем ее приближенно равной цене за год до погашения облигации). Если ожидаемая доходность по таким облигациям равна 8%, то

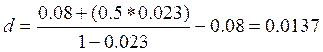
Таким образом, премия за возможность неплатежа равна 137 базисных пунктов.

1.5.7. Горизонтный анализ

Для анализа выбирается определенный период и рассматривается временная структура процентных ставок на конец этого периода. Затем анализируются две облигации - та, которая находится во владении и та, которая является кандидатом для замены. Предполагается, что риска возможной неуплаты для обеих облигаций не существует.

Предположим, облигация продается по текущей цене P_o, ее доходность - y_o. В качестве периода анализа принимается H лет. Через H лет облигация будет продана по цене P_h с приведенной доходностью y_h. Рассмотрим для примера четырехпроцентную облигацию, данные по которой приведены в табл. 1.11.

Таблица 1.11