Анализ простых облигаций, их доходность, форвардная ставка процента, страница 4

Таблица 1.7

Временная  структура процентных ставок

В верхней части таблицы показана условная структура процентных ставок на 01.01.1997 г. Будущая ставка для любого года зависит от двух элементов. Во-первых, это ожидаемая в будущем текущая процентная ставка за соответствующий год. Во-вторых, это премия за ликвидность, которая является возрастающей функцией числа лет между текущим и будущим годом. Для упрощения расчетов премия выражается с помощью коэффициента. Если, например, в 1997 году ожидаемая текущая ставка в 1999 году равна 7%, коэффициент премии за ликвидность - 1.004, то будущая процентная ставка для этого года равна 7.428% (1.07*1.004).

Вторая (нижняя) часть табл.1.7 показывает процентные ставки для следующего года при неизменных условиях. Фактическая текущая процентная ставка в 1998 году равна соответствующей ожидаемой процентной ставке в 1997 году, а ожидаемые текущие процентные ставки для 1999 и 2000 года не изменились (как и коэффициенты премии за ликвидность).

Рассмотрим теперь как изменится цена на долгосрочную облигацию между 01.01.1997 г. и 01.01.1998 г. Для простоты возьмем дисконтную облигацию со сроком погашения в конце 2000 г. Ее стоимость на начало 1997 года будет равна:

.

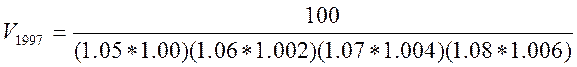В начале следующего года:

.

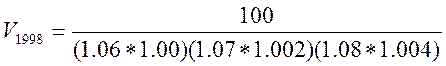Знаменатели этих дробей отличаются тем, что в первой дроби одним из множителей является текущая процентная ставка в 1997 году и коэффициент премии за ликвидность для четвертого года. Таким образом,

V₁₉₉₈=V₁₉₉₇*1.05*1.006=V₁₉₉₇*1.0563

При условиях этого примера долгосрочная дисконтная облигация обеспечит большую доходность, чем краткосрочная дисконтная облигация. Разница определяется коэффициентом премии за ликвидность. Поскольку средне- и долгосрочные купонные облигации эквивалентны пакету годовых дисконтных облигаций, то их годовая доходность превышает годовую доходность одногодичных облигаций. Эта разница тем больше, чем больше разница в сроке их погашения.

1.5.4. Доходность выкупных облигаций

Предположим, в 1992 году выпущены шестипроцентные облигации с погашением в 2025 году. Облигации проданы по цене 89 рублей. Доходность по ним - 6.84%.

Однако, облигации были выкуплены в 2000 году за 104 рубля. Для расчета влияния этого мероприятия на доходность, рассчитывается доходность до момента выкупа (yiеld-to-first-call). Таким образом, облигация связана с такими платежами (см.табл. 1.8):

Таблица 1.8

Взаимосвязь цены облигации с платежами

Доходность, рассчитанная по этим данным, и будет доходностью до выкупа. Она равна 8.27%, что превышает доходность до погашения для этой облигации.

Для определения целесообразности выкупа облигации, рассчитывают ее доходность от выкупа до погашения. Предполагается, что шестипроцентная облигация номиналом 100 рублей с погашением в 2025 году куплена в 2000 году за 104 рубля. Доходность от выкупа до погашения равна 5.70%.