Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 9

1.  Обработаем первую серию экспериментальных данных    (таблица 8).

Среднее арифметическое результата первой серии измерений:

=8,346

Стандартное отклонение результата первой серии измерений. Вспомогательные вычисления сведены в 3 и 4 графы таблицы 8.

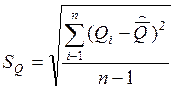
Больше чем на 3=0,054 от среднего арифметического не отличается ни одно из оставшихся значений Q.

Таблица 8.

i		-	(- )²
1	2	3	4
1	8,34	-0,006	0,000036
2	8,32	-0,026	0,000676
3	8,34	-0,006	0,000036
4	8,33	-0,016	0,000256
5	8,35	0,004	0,000016
6	8,36	0,014	0,000196
7	8,34	-0,006	0,000036
8	8,32	-0,026	0,000676
9	8,34	-0,006	0,000036
10	8,36	0,014	0,000196
11	8,37	0,024	0,000576
12	8,35	0,004	0,000016
13	8,38	0,034	0,001156

Проверим с помощью составного критерия справедливость сделанного допущения.

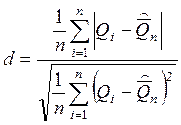
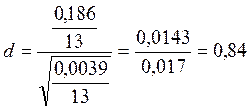
Проверим выполнение условия

Условие 0,6675 ≤ d ≤ 0,9359 соблюдается с вероятностью Р*= 0,99.

Так как это условие выполняется, то дополнительно проверим «хвосты» теоретического и эмпирического законов распределения вероятности. При 10 ≤ n ≤ 20 считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5, что соответствует доверительной вероятности Р**= 0,98.

Так как =0,017, то следует, что ни один результат измерения  не отличается от  больше, чем на 2,5 =0,043.

Следовательно, гипотеза о нормальности распределения вероятности результата измерения может быть принята с вероятностью P ≥ Р*+Р**–1 ≥ 0,99+0,98–1 ≥ 0,97.

2.  Обработаем вторую серию экспериментальных данных    (таблица 9).

Исходя из того, что в подавляющем большинстве случаев результат измерения подчиняется нормальному закону распределения вероятности, исключим по правилу трех сигм ошибки, если они есть.

Среднее арифметическое результата второй серии измерений:

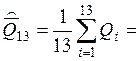8,343

Стандартное отклонение результата второй серии измерений. Вспомогательные вычисления сведены в 3 и 4 графы таблицы 9.

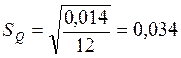
Больше чем на 3=0,1 от среднего арифметического отличается   i=12. Следовательно, это значение являются ошибочными и должно быть отброшено.

Таблица 8

i
1	2	3	4	5	6
1	8,35	0,007	0,000049	0,016	0,000256
2	8,33	-0,013	0,000169	-0,004	0,000016
3	8,33	-0,013	0,000169	-0,004	0,000016
4	8,34	-0,003	0,000009	0,006	0,000036
5	8,33	-0,013	0,000169	-0,004	0,000016
6	8,33	-0,013	0,000169	-0,004	0,000016
7	8,34	-0,003	0,000009	0,006	0,000036
8	8,34	-0,003	0,000009	0,006	0,000036
9	8,34	-0,003	0,000009	0,006	0,000036
10	8,31	-0,033	0,001089	-0,024	0,000576
11	8,32	-0,023	0,000529	-0,014	0,000196
12	8,45	0,007	0,011449
13	8,35	0,007	0,000049	0,016	0,000256