Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 12

Так как 0,018 , то следует, что ни один результат измерения  не отличается от  больше, чем на 2,5= 0,045.

Следовательно, гипотеза о нормальности распределения вероятности результата измерения может быть принята с вероятностью P ≥ Р*+Р**–1 ≥ 0,99+0,98–1 ≥ 0,97.

Обработаем вторую серию экспериментальных данных    (таблица 12).

Среднее арифметическое результата второй серии измерений:

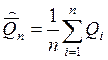
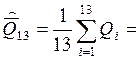8,445

Стандартное отклонение результата второй серии измерений. Вспомогательные вычисления сведены в 3 и 4 графы таблицы 12.

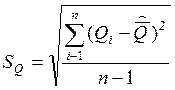
Таблица 12

i
1	2	3	4
1	8,43	-0,015	0,000225
2	8,45	0,005	0,000025
3	8,42	-0,025	0,000625
4	8,45	0,005	0,000025
5	8,44	-0,005	0,000025
6	8,46	0,015	0,000225
7	8,44	-0,005	0,000025
8	8,45	0,005	0,000025
9	8,46	0,015	0,000225
10	8,49	0,045	0,002025
11	8,42	-0,025	0,000625
12	8,44	-0,005	0,000025
13	8,44	-0,005	0,000025

Больше чем на 3=0,055 от среднего арифметического не отличается ни одно из оставшихся значений Q.

Проверим с помощью составного критерия справедливость сделанного допущения.

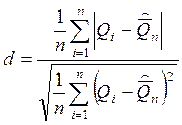
Проверим выполнение условия

Условие 0,6675 ≤ d ≤ 0,9359 соблюдается с вероятностью Р* = 0,99.

Так как это условие выполняется, то дополнительно проверим «хвосты» теоретического и эмпирического законов распределения вероятности. При 10 ≤ n ≤ 20 считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5, что соответствует доверительной вероятности Р**=0,98.

Больше чем на 0,046 от среднего арифметического не отличается ни одно значение.

Следовательно, гипотеза о нормальности распределения вероятности результата измерения может быть принята с вероятностью P ≥ Р*+Р**–1 ≥ 0,99+0,98–1 ≥ 0,97.

Продолжим проверку серий на однородность.

Сравним между собой средние арифметические и оценки дисперсий в каждой серии.

Таблица 13

I серия измерений	II серия измерений

Проверим значимость различия между средними арифметическими в двух сериях.

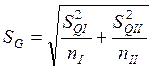
Зададим доверительную вероятность Р*=0,99 , используя график на рис.22 [1], с.58 по верхней кривой определим соответствующее ей значение t=2,6.

0,103 > 0,019

Следовательно, различие между средними арифметическими в сериях считается значимым.

Соответственно серии неоднородны.

Список используемой литературы

Шишкин И.Ф. Теоретическая метрология: Учебник для вузов. – М.: Изд-во стандартов, 1991.

Шишкин И.Ф. Теоретическая метрология. Ч.1. Общая теория измерений: Учеб.-метод. комплекс. – СПб.: Изд-во СЗТУ, 2008.

Помелов И.С. Оценка точности результатов измерений. Методические указания к выполнению лабораторных работ. Белорусская государственная сельскохозяйственная академия. – Горки, 2007