Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 6

Найдем длину интервала по формуле

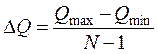, где N – количество интервалов.

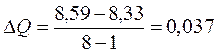
Данные представим в виде вспомогательной таблицы 6.

Таблица 6

Рисунок 4. Гистограмма

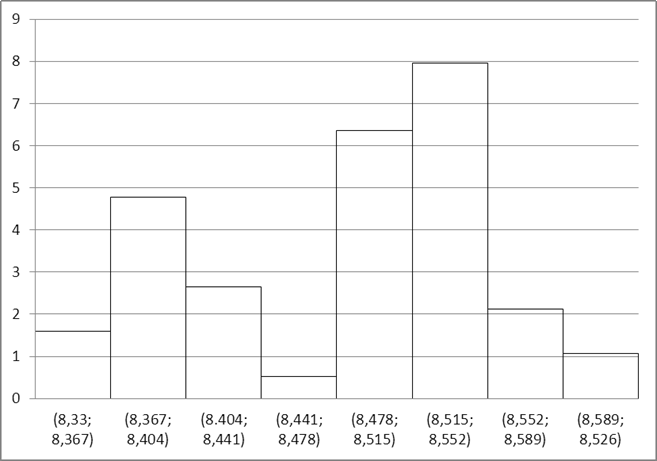
Анализ априорной информации и вид гистограммы массива экспериментальных данных позволяет утверждать, что результат измерения не подчиняется нормальному закону распределения вероятности.

Вид построенной гистограммы  может свидетельствовать о том, что возможной теоретической моделью данного распределения может служить двухмодальный закон распределения вероятности.

Соответственно, заменяя среднее квадратическое отклонение среднего арифметического его оценкой, найдем стандартное отклонение среднего арифметического:

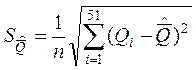
= 0,011

Задавшись доверительной вероятностью Р=0,85 по нижней кривой на рис.22 [1], с.58 определим t=2,6.

Рассчитаем половину доверительного интервала:

= 2,6·0,011 = 0,029

Пределы, в которых находится значение измеренной величины устанавливаются по формуле:

8,452 ≤ Q ≤ 8,510

2.4 Обработка результатов многократных измерений с неравноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности.

Длина измерена средствами измерений с разными классами точности и полученные данные приведены в таблице 7.

Таблица 7

Порядковый номер измерения	Первое СИ	Второе СИ	Третье СИ
1	2	3	4
1	8,335	8,34	8,34
2	8,34	8,35	8,35
3	8,34	8,36	8,35
4	8,35	8,36	8,36
5	8,35	8,36	8,36
6	-	8,37	8,36
7	-	8,37	8,36
8	-	8,38	8,36
9		-	8,37
10		-	8,37
11		-	8,37
12		-	8,37
13		-	8,37
14		-	8,37
15		-	8,37
16		-	8,38
17		-	8,38
18		-	8,38
19		-	8,39
20		-	8,39
21		-	8,40

а) Проанализируем результат измерения первым средством измерения.

Среднее арифметическое результата измерений:

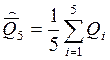= 8,343

Стандартное отклонение результата измерений.

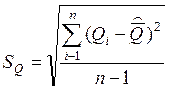
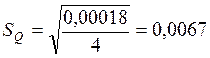
Больше чем на 3=0,02 от среднего арифметического не отличается ни одно из значений. Следовательно, среди них нет ошибочных.

При n<10…15 гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, не проверяется.

На основании априорной информации и сделанных вычислений делаем вывод, что результат измерения первым СИ подчиняется нормальному закону распределения вероятности со стандартным отклонением 0,0067.

б) Проанализируем результат измерения вторым средством измерения.