Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 4

i	Интервалы
1	2	3	4	5	6	7	8
1	[- ∞; 8,355]	5	-1,36	-0,4161	0,0839	0,5533	0,07
2	[8,355; 8,365]	5	-0,82	-0,2939	0,1222	-1,4766	0,34
3	[8,365; 8,375]	7	-0,27	-0,1064	0,1875	-2,9375	0,87
4	[8,375; 8,385]	17	0,27	0,1064	0,2128	5,7216	2,9
5	[8,385; 8,395]	9	0,82	0,2939	0,1875	-0,9375	0,09
6	[8,395; 8,405]	5	1,36	0,4161	0,1222	-1,4766	0,34
7	[8,405; + ∞]	5	+ ∞	0,5	0,0839	0,5533	0,07

Определим, на сколько  отстоит от среднего арифметического значения правая граница каждого интервала:

Полученные значения округлим до двух знаков после запятой и внесем в четвертую графу таблицы 4.

По значению  можно определить, с какой вероятностью отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, попадает в интервал (). Эта вероятность определяется интегралом вероятности – функцией Лапласа . Полученные значения  занесены в пятую графу таблицы 4.

Теоретическая вероятность  попадания в i-й интервал отдельного значения результата измерения, подчиняющегося нормальному закону распределения вероятности, равна . Полученные расчетные значения  сведены в шестую графу таблицы 4, при этом помним, что L(-∞) = – 0,5 , а  L(+∞) = + 0,5.

В седьмую и восьмую графы таблицы 4 внесены результаты остальных вспомогательных вычислений. Суммирование чисел в восьмой графе дает

χ²= 4,67.

Из графика [1], с.87, рис.35 видно, что рассчитанное значение 2,01 <  для вероятности Р*=0,95. Таким образом, с вероятностью Р*=0,95 можно принять гипотезу о том, что результат измерения подчиняется нормальному закону.

Стандартное отклонение среднего арифметического в каждом из трех массивов экспериментальных данных:

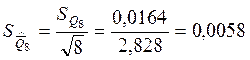
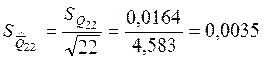
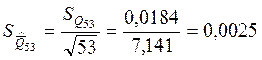
Для анализа зависимости точности результата многократного измерения от объема экспериментальных данных построим график зависимости  от числа измерений n.

Как видно на рисунке, при увеличении объема экспериментальных данных точность результата многократного измерения повышается.

Пределы, в которых находится значение измеренного периметра помещения, устанавливаются по формуле:

где ε=, а коэффициент Стьюдента t зависит от доверительной вероятности P. Используя график на рис.38 [1], с.93 определим коэффициенты Стьюдента при Р=0,95 получаем

t = 2,5                ε = 2,5·0,0058 = 0,015

t = 2,2                ε = 2,2·0,0035 = 0,008

t = 2,0                ε = 2,0·0,0025 = 0,005

Отсюда:

Q = 8,364…..8,394         при n = 8;

Q = 8,359…..8,375         при n = 22;

Q = 8,375…..8,385        при n = 53.

Вывод: точность определения значений измеряемой величины повышается при увеличении числа измерений. Используя массив экспериментальных данных, можно определить числовые характеристики закона распределения вероятности результата измерения, а также  пределы, в которых они находятся с определенной вероятностью.

2.3 Обработка результатов многократных измерений с равноточными значениями отсчета, не подчиняющихся нормальному закону распределения вероятности.

При измерении получен следующий массив экспериментальных данных:

8,58; 8,55; 8,54; 8,48; 8,50; 8,52; 8,51; 8,52; 8,52; 8,51; 8,52; 8,48; 8,49; 8,48; 8,51; 8,53; 8,58; 8,59; 8,55; 8,53; 8,59; 8,58; 8,55; 8,57; 8,55; 8,55; 8,50; 8,51; 8,53; 8,51; 8,54; 8,51; 8,46; 8,44; 8,42; 8,41; 8,55; 8,37; 8,38; 8,39; 8,37; 8,40; 8,41; 8,37; 8,40; 8,41; 8,39; 8,34; 8,33; 8,35; 8,37.