Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 11

Проверка однородности является обязательной при выборе способа совместной обработки результатов измерений. Серии называются однородными, если состоят из значений, подчиняющихся одному и тому же закону распределения вероятности и соблюдаются два условия: незначимое различие между средними арифметическими в двух сериях, равнорассеянность серий. В противном случае серии считаются неоднородными.

Обработаем первую серию экспериментальных данных    (таблица 11).

Исходя из того, что в подавляющем большинстве случаев результат измерения подчиняется нормальному закону распределения вероятности, исключим по правилу трех сигм ошибки, если они есть.

Среднее арифметическое результата первой серии измерений:

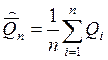
Стандартное отклонение результата первой серии измерений. Вспомогательные вычисления сведены в 3 и 4 графы таблицы 11.

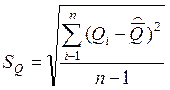
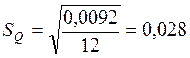
Больше чем на 3=0,084 от среднего арифметического отличается   i=11. Следовательно, это значение являются ошибочными и должно быть отброшено.

Таблица 11

i
1	2	3	4	5	6
1	8,34	-0,008	0,000064	-0,002	0,000004
2	8,35	0,002	0,000004	0,008	0,000064
3	8,37	0,022	0,000484	0,028	0,000784
4	8,33	-0,018	0,000324	-0,012	0,000144
5	8,32	-0,028	0,000784	-0,022	0,000484
6	8,34	-0,008	0,000064	-0,002	0,000004
7	8,32	-0,028	0,000784	-0,022	0,000484
8	8,33	-0,018	0,000324	-0,012	0,000144
9	8,34	-0,008	0,000064	-0,002	0,000004
10	8,34	-0,008	0,000064	-0,002	0,000004
11	8,42	0,072	0,005184
12	8,33	0,032	0,001024	0,038	0,001144
13	8,34	-0,008	0,000064	-0,002	0,000004

После внесения поправок:

8,342

Повторно определим стандартное отклонение результата первой серии измерений. Вспомогательные вычисления сведены в 5 и 6 графы таблицы 11.

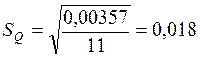
Больше чем на 3=0,054 от среднего арифметического не отличается ни одно из оставшихся значений Q. Следовательно, можно считать, что среди них нет ошибочных.

Поскольку n=12 проверим с помощью составного критерия справедливость сделанного допущения о нормальности закона распределения вероятности относительно первой серии измерений.

Сначала рассчитаем:

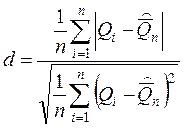
и проверим выполнение условия .

Если это условие выполняется, то дополнительно проверим «хвосты» теоретического и эмпирического законов распределения вероятности. При 10 ≤ n ≤ 20 считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5.

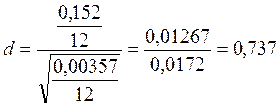
Проверяем выполнение условия

Условие 0,6675 ≤ d ≤ 0,9359 соблюдается с вероятностью Р*= 0,99.

Так как это условие выполняется, то дополнительно проверим «хвосты» теоретического и эмпирического законов распределения вероятности. При 10 ≤ n ≤ 20 считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5, что соответствует доверительной вероятности Р**=0,98.