Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 2

Проверим массивы экспериментальных данных на наличие промахов по «правилу трех сигм». Больше чем на  от среднего арифметического не отличается ни одно из Q.

Следовательно, можно считать, что среди них нет ошибочных.

Для получения представления о характере закона распределения вероятности результата измерений построим гистограмму для второго и третьего массивов экспериментальных данных.

Для построения гистограммы необходимо выбрать оптимальное число интервалов группирования экспериментальных данных.

Для правильности отображения гистограммой характера закона распределения вероятности нужно соблюдать следующие правила:

Интервалы ∆Q следует выбирать одинаковыми.

Так как предполагается, что закон распределения плотности вероятности симметричный, то желательно, чтобы количество интервалов было нечетным.

Масштаб выбирать таким. Чтобы высота гистограммы относилась к ее основанию как 5 к 8.

Найдем длину интервала по формуле

, где N – количество интервалов.

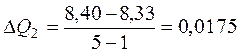
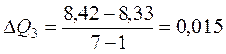
Данные представим в виде вспомогательной таблицы 2.

Таблица 2

Интервалы
1	2	3
Массив 2
8,33….8,3475	2	5,2
8,3475….8,365	7	18,2
8,365….8,3825	10	26
8,3825….8,40	2	5,2
8,40…8,4175	1	2,6
Массив 3
8,33….8,345	2	2,5
8,345….8,36	3	3,8
8,36….8,375	12	15,1
8,375….8,39	17	21,4
8,39….8,405	14	17,6
8,405….8,42	4	5,0
8,42….8,435	1	1,3

Рисунок 1. Гистограмма для второго массива экспериментальных данных.

Рисунок 2. Гистограмма для третьего массива экспериментальных данных.

Анализ априорной информации и вид гистограмм массивов экспериментальных данных позволяет предположить, что результат измерения подчиняется нормальному закону распределения вероятности.

При n<10…15 гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, не проверяется.

При 10…15<n<40…50 для проверки гипотезы о нормальности закона распределения вероятности используется составной критерий.

При n>40…50 при проверке гипотезы о соответствии экспериментальных данных нормальному закону распределения вероятности измерений используется критерий Пирсона.

Поскольку n=22 проверим с помощью составного критерия справедливость сделанного допущения относительно второго массива экспериментальных данных.

Сначала рассчитаем:

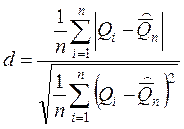
и проверим выполнение условия .

Если это условие выполняется, то дополнительно проверим «хвосты» теоретического и эмпирического законов распределения вероятности. При 10 ≤ n ≤ 20 считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5.

Результаты вспомогательных расчётов сведем в таблицу 3.

Таблица 3