Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 10

После внесения поправок:

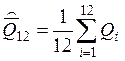=8,334

Повторно определим стандартное отклонение результата второй серии измерений. Вспомогательные вычисления сведены в 5 и 6 графы таблицы 8.

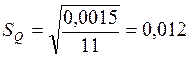
Больше чем на 3=0,036 от среднего арифметического не отличается ни одно из оставшихся значений Q. Следовательно, можно считать, что среди них нет ошибочных.

Поскольку n=12 проверим с помощью составного критерия справедливость сделанного допущения о нормальности закона распределения вероятности относительно второй серии измерений.

Сначала рассчитаем:

и проверим выполнение условия .

Если это условие выполняется, то дополнительно проверим «хвосты» теоретического и эмпирического законов распределения вероятности. При 10 ≤ n ≤ 20 считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5.

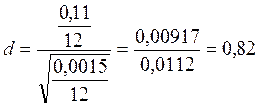
Проверяем выполнение условия

Условие 0,6675 ≤ d ≤ 0,9359 соблюдается с вероятностью Р* = 0,99.

Так как это условие выполняется, то дополнительно проверим «хвосты» теоретического и эмпирического законов распределения вероятности. При 10 ≤  n ≤ 20 считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5, что соответствует доверительной вероятности Р**=0,98.

Так как =0,012, то следует, что ни один результат измерения  не отличается от  больше, чем на 2,5 =0,03.

Следовательно, гипотеза о нормальности распределения вероятности результата измерения может быть принята с вероятностью P ≥ Р*+Р**–1 ≥ 0,99+0,98–1 ≥ 0,97.

Продолжим проверку серий на однородность.

Сравним между собой средние арифметические и оценки дисперсий в каждой серии.

Таблица 10

I серия измерений	II серия измерений

Проверим значимость различия между средними арифметическими в двух сериях.

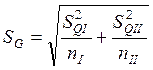
Зададим доверительную вероятность Р*=0,99, используя график на рис.22 [1], с.58 по верхней кривой определим соответствующее ей значение t=2,6.

0,012<0,016

Следовательно, различие между средними арифметическими в сериях считается незначимым.

Проверим равнорассеянность результатов измерений в двух сериях. Для этого должно соблюдаться условие:

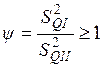
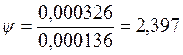
Выбираем вероятность Р=0,95, с которой будет приниматься решение и определяем значение аргумента  интегральной функции распределения вероятности Р.А. Фишера, равный 2,69.

Так как , то различие оценок дисперсий в сериях можно признать случайными с вероятностью Р=0,95 считать, что гипотеза о равнорассеянности серий не противоречит результатам ее проверки по критерию Р.А. Фишера. Серии равнорассеяны.

Равнорассеянные серии с незначимым различием между средними арифметическими считаются однородными. Экспериментальные данные, входящие в однородные серии, можно рассматривать и обрабатывать как единый массив.

Выполним обработку экспериментальных данных, входящих в однородные серии.

Оценка среднего значения результата измерения:

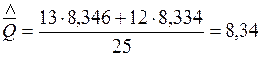
Стандартное отклонение среднего арифметического:

Пределы, в которых находится значение измеренного устанавливаются по формуле:

 с доверительной вероятностью Р=0,97.

2.7 Обработка 2 результатов многократных измерений, полученных в двух неоднородных сериях.

При измерении массы получены следующие две серии экспериментальных данных, в граммах:

1 серия: 8,34; 8,35; 8,37; 8,33; 8,32; 8,34; 8,32; 8,33; 8,34; 8,34; 8,42; 8,33; 8,34.

2 серия: 8,43; 8,45; 8,42; 8,45; 8,44; 8,46; 8,44; 8,45; 8,46; 8,49; 8,42; 8,44; 8,44.