Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 3

На основании выполненных расчетов:

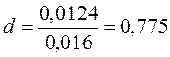
Условие 0,6950 ≤ d ≤ 0,9001 соблюдается с вероятностью Р* = 0,99.

При 10 ≤ n ≤ 20 считается допустимым отклонение одного из независимых значений результата измерения от среднего арифметического больше чем на 2,5, что соответствует доверительной вероятности Р**=0,98.

Так как

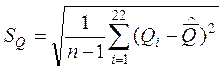= 0,0164

то из второго столбца таблицы следует, что ни один результат измерения  не отличается от  больше, чем на 2,5· = 0,041.

Следовательно, гипотеза о нормальности распределения вероятности результата измерения может быть принята с вероятностью P ≥ Р*+Р**–1 ≥ 0,99+0,98–1 ≥ 0,97.

Выражение для плотности распределения вероятности результата измерения, подчиняющегося нормальному закону, имеет вид

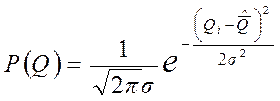
При σ =  получим 

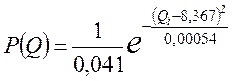
Результаты расчёта приведены в таблице 1.3.

Таблица 1.3

По данным таблицы построим график плотности распределения вероятности результата измерения.

Результат измерения является случайным. Он подчиняется закону распределения вероятности с оценками числовых характеристик = 8,367  м,  = 0,0164  м.

Проверим гипотезу о соответствии экспериментальных данных третьего массива экспериментальных данных нормальному закону распределения вероятности с помощью критерия Пирсона.

При использовании критерия К. Пирсона в каждом интервале должно быть не меньше пяти независимых значений результата измерения. В соответствии с этим образуем, интервалы так, как это представлено во второй графе таблицы 4.

Таблица 4