Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 7

Среднее арифметическое результата измерений:

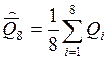= 8,361

Стандартное отклонение результата измерений.

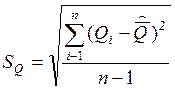
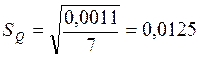
Больше чем на 3=0,038 от среднего арифметического не отличается ни одно из значений. Следовательно, среди них нет ошибочных.

При n<10…15 гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, не проверяется.

На основании априорной информации и сделанных вычислений делаем вывод, что результат измерения вторым СИ подчиняется нормальному закону распределения вероятности со стандартным отклонением 0,0125.

в) Проанализируем результат измерения третьим средством измерения.

Среднее арифметическое результата измерений:

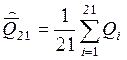= 8,369

Стандартное отклонение результата измерений.

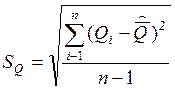
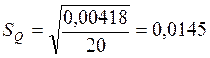
Больше чем на 3=0,044 от среднего арифметического не отличается ни одно из значений. Следовательно, среди них нет ошибочных.

При 10…15 < n < 40…50  для проверки гипотезы о нормальности закона распределения  вероятности используется составной критерий.

Сначала рассчитаем:

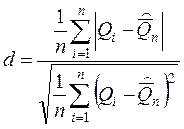
и проверим выполнение условия .

На основании выполненных расчетов:

= 0,759

Условие 0,6950<d<0,9001 соблюдается с вероятностью Р*= 0,99.

Так как это условие выполняется, то дополнительно проверим «хвосты» теоретического и эмпирического законов распределения вероятности. При 20≤ n≤ 50 считается допустимым отклонение двух из независимых значений результата измерения от среднего арифметического больше чем на 2,5.

При n=21 считается допустимым отклонение не более двух из независимых значений результата измерения от среднего арифметического больше чем на 2,5, что соответствует доверительной вероятности Р**=0,98.

Так как

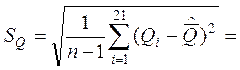0,0145

то из второго столбца таблицы следует, что ни один результат измерения  не отличается от  больше, чем на 2,5= 0,036.

Следовательно, гипотеза о нормальности распределения вероятности результата измерения может быть принята с вероятностью Р = Р* + Р** – 1 = 0,99 + 0,98 – 1 = 0,97.

Отсюда следует вывод, что результат измерения третьим СИ подчиняется нормальному закону распределения вероятности со стандартным отклонением 0,0145.

При многократном измерении с неравноточными значениями отсчета, подчиняющимися нормальному закону распределения вероятности, используется среднее взвешенное, в числителе которого отдельные значения результата измерения суммируются с «весами», обратно пропорциональными их дисперсиям. Тем самым более точным значениям придается больший вес.

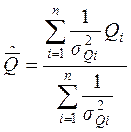
Заменяя дисперсии их оценками, имеем:

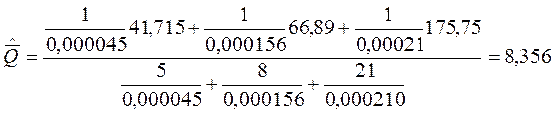
Стандартное отклонение:

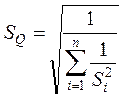
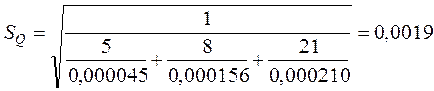
Поскольку все  подчиняются нормальному закону распределения вероятности, то нормальному закону подчиняется и их сумма. Поэтому с вероятностью Р=0,97, используя график на рис.38 [1], с.93 определим коэффициент Стьюдента t=2,2.

Предел, в котором находится значение измеренной величины:

, где , а коэффициент Стьюдента t зависит от доверительной вероятности P.

ε=2,2·0,0019=0,0042

8,352≤Q≤8,360

2.5 Обработка результатов многократных измерений с неравноточными значениями отсчета, не подчиняющихся нормальному закону распределения вероятности.

Длина измерена средствами измерений с разными классами точности и полученные данные приведены в таблице 7.

Таблица 7

Порядковый номер измерения	Первое СИ	Второе СИ	Третье СИ
1	2	3	4
1	8,37	8,37	8,37
2	8,37	8,37	8,37
3	8,39	8,38	8,37
4	8,40	8,40	8,37
5	8,40	8,41	8,38
6	-	8,41	8,39
7	-	8,42	8,40
8	-	8,42	8,40
9		8,43	8,41
10		-	8,41
11		-	8,41
12		-	8,42
13		-	8,44
14		-	8,46
15		-	8,46
16		-	8,48
17		-	8,48
18		-	8,48
19		-	8,48
20		-	8,50
21		-	8,50
22			8,51