Обработка 3 результатов многократных измерений с равноточными значениями отсчета, подчиняющихся нормальному закону распределения вероятности, страница 8

а) Проанализируем результат измерения первым средством измерения.

Среднее арифметическое результата измерений:

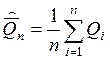
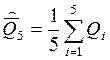= 8,386

Стандартное отклонение результата измерений.

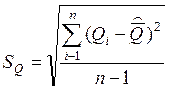
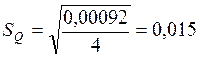
Больше чем на 3=0,045 от среднего арифметического не отличается ни одно из значений. Следовательно, среди них нет ошибочных.

При n<10…15 гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, не проверяется.

б) Проанализируем результат измерения вторым средством измерения.

Среднее арифметическое результата измерений:

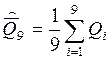= 8,402

Стандартное отклонение результата измерений.

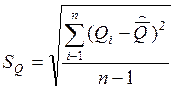
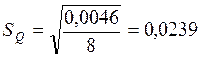
Больше чем на 3=0,072 от среднего арифметического не отличается ни одно из значений. Следовательно, среди них нет ошибочных.

При n<10…15 гипотеза о том, что результат измерения подчиняется нормальному закону распределения вероятности, не проверяется.

в) Проанализируем результат измерения третьим средством измерения.

Среднее арифметическое результата измерений:

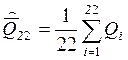= 8,431

Стандартное отклонение результата измерений.

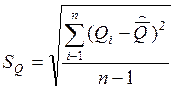
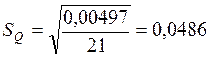
Больше чем на 3=0,146 от среднего арифметического не отличается ни одно из значений. Следовательно, среди них нет ошибочных.

Для получения представления о характере закона распределения вероятности результата измерений построим гистограмму для третьего массива экспериментальных данных.

Найдем длину интервала по формуле

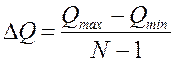, где N – количество интервалов.

Данные представим в виде вспомогательной таблицы 2.

Таблица 2

Рисунок 1. Гистограмма для третьего массива экспериментальных данных.

При 10…15 < n < 40…50  для проверки гипотезы о нормальности закона распределения  вероятности используется составной критерий.

Сначала рассчитаем:

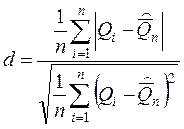
и проверим выполнение условия .

На основании выполненных расчетов:

= 0,905

Условие 0,6950<d<0,9001 не соблюдается.

Так как это условие не выполняется, следовательно гипотеза о нормальности закона распределения не подтверждается.

Анализ априорной информации и вид гистограммы массива экспериментальных данных позволяет утверждать, что результат измерения не подчиняется нормальному закону распределения вероятности.

Вид построенной гистограммы  может свидетельствовать о том, что возможной теоретической моделью данного распределения может служить одномодальный закон распределения вероятности.

Соответственно, заменяя среднее квадратическое отклонение среднего арифметического его оценкой, найдем стандартное отклонение среднего арифметического:

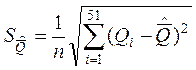
= 0,0101

Задавшись доверительной вероятностью Р=0,85 по нижней кривой на рис.52 [1], с.120 определим t=2,6.

Рассчитаем половину доверительного интервала:

= 2,6·0,0101 = 0,026

Пределы, в которых находится значение измеренной величины устанавливаются по формуле:

8,405 ≤ Q ≤ 8,457

2.6 Обработка 2 результатов многократных измерений, полученных в двух однородных сериях.

При измерении массы получены следующие две серии экспериментальных данных, в граммах:

1 серия: 8,34; 8,32; 8,34; 8,33; 8,35; 8,36; 8,34; 8,32; 8,34; 8,36; 8,37; 8,35; 8,38.

2 серия: 8,35; 8,33; 8,33; 8,34; 8,33; 8,33; 8,34; 8,34; 8,34; 8,31; 8,32; 8,45; 8,35.

Проверка однородности является обязательной при выборе способа совместной обработки результатов измерений. Серии называются однородными, если состоят из значений, подчиняющихся одному и тому же закону распределения вероятности и соблюдаются два условия: незначимое различие между средними арифметическими в двух сериях, равнорассеянность серий. В противном случае серии считаются неоднородными.