Описание производства асбестоцементных изделий, страница 16

Связанные системы регулирования включают кроме основных регуляторов дополнительные динамические компенсаторы. Расчет и наладка таких систем гораздо сложнее, чем одноконтурных АСР, что препятствует их широкому применению в промышленных системах автоматизации.

Рассмотрим методы расчета многосвязных систем регулирования на примере объекта с двумя входами и двумя выходами.

3.1.1.Синтез несвязанного регулирования

Структурная схема системы представлена на рисунке 3.1 Преобразование системы регулирования двух координат к эквивалентным одноконтурным АСР дано на рисунке 3.2

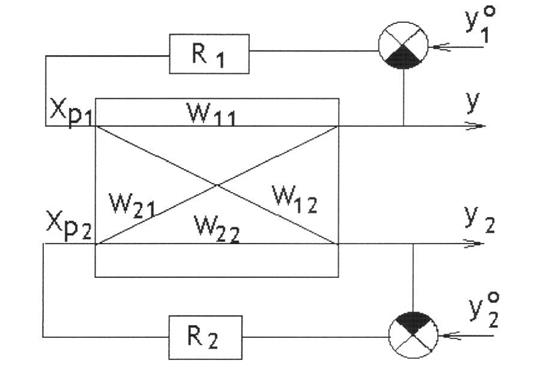
Рисунок 3.1 - Структурная схема несвязного регулирования со взаимосвязанными координатами

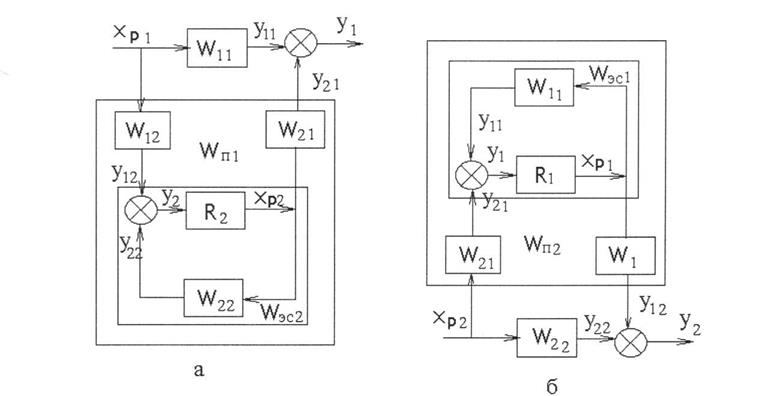
Рисунок 3.2 - Преобразование системы регулирования двух координат к эквивалентным одноконтурным АСР

а - эквивалентный объект для первого  регулятора; б - эквивалентный объект для второго регулятора.

Выведем передаточную функцию эквивалентного объекта в одноконтурной АСР с регулятором R1. Как видно, такой объект состоит из основного канала регулирования и связанной с ним параллельно сложной системы, включающей второй замкнутый контур регулирования и два перекрестных канала объекта. Передаточная функция эквивалентного, объекта имеет вид:

 ;                   

Второе слагаемое в правой части уравнения (7) отражает влияние второго контура регулирование на рассматриваемую и по существу является корректирующей поправкой к передаточной функции прямого канала.

Аналогично для второго эквивалентного объекта  получим передаточную функцию в виде:

                                  

На основе формул можно предположить, что если на какой-то частоте модуль корректирующей поправки будет пренебрежимо мал по сравнению с амплитудно-частотной характеристикой прямого канала, поведение эквивалентного объекта на этой частоте будет определятся прямым каналом.

Наиболее важно значение поправки на рабочей частоте каждого контура. В частности, если рабочие частоты двух контуров регулирования co_pi и оз_р2 существенно различны, то можно ожидать, что взаимное влияние их будет незначительным при условии:

|W_п2(iω_pl)| << |W₁₁(iω_pl)| ;     (9)

Где |W_п2(iω_pl)| =

Наибольшую опасность представляет случай, когда инерционность прямых и перекрестных каналов приблизительно одинакова. Пусть например, Wn(p)=W12(p)=W21(p)=W22(p)=W(p). Тогда для эквивалентных объектов при условии, что R1(p)=R2(p)=R(p), получим передаточные функции:

    ; (10)

частотные характеристики

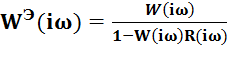                                                  (11) 

На границе устойчивости, согласно критерию Найквиста получим:

       или        ;               (12)

Откуда      =l или |R(iω)|=0.5/|W(iω)|

Так, настройка П - регулятора, при которой система находится на границе устойчивости, вдвое меньше, чем в одноконтурной АСР.

Для качественной оценки взаимного влияния контуров регулирования используют комплексный коэффициент связанности:

  ;(13)

который обычно вычисляют при нулевой частоте (т.е. в установившихся режимах) и на рабочих частотах регуляторов co_pi и со_Р2. В частности, при ш=0 значение кс_В определяется отношением коэффициентов усиления по перекрестным и основным каналам:

ксв (0)=Ri2 R21 /(R11 R22); (14) Если на этих частотах кс_В =0, то объект можно рассматривать как односвязный, при кс_В>1 целесообразно поменять местами прямые и перекрестные каналы; 0<кс_В<1 расчет одноконтурных АСР необходимо вести по передаточным функциям эквивалентных объектов (7) и (8).

Рассчитаем кс_В для нашего варианта:

kcв⁼(ki2*k2i)/(k11*k22)=(0.47*0.0085)/(0.015*3.25)~0.11

 

3.1.2 Системы связанного регулирования

На рисунке 8 представлены структурные схемы автономных АСР

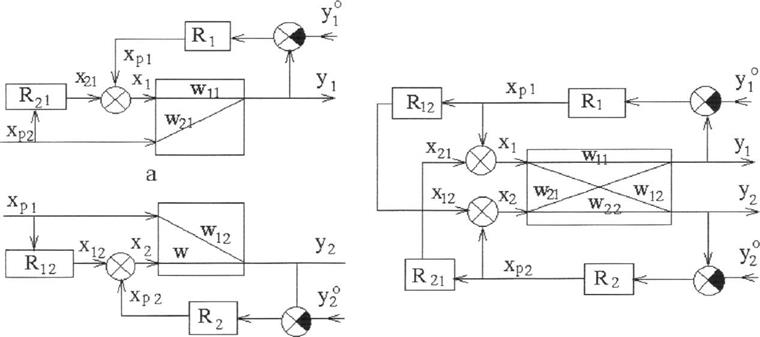
Рисунок 3.3 – структурные схемы автономных АСР

а - компенсация воздействий от второго регулятора в первом контуре регулирования;

б - компенсация воздействий от первого регулятора во втором контуре регулирования;

в - автономная система регулирования двух координат. Рисунок Рисунок 8 - Структурные схемы автономных АСР