Результатом решения данного уравнения будут две функции: ω1(t) и φ1(t). Из них время можно исключить как параметр: ω1(φ).
Для обеспечения требуемой плавности хода многократно решается уравнение движения по алгоритму представленному на рис. 8.1. В процессе его реализации варьируется значение момента инерции маховика, входящей константой в приведенный момент, и контролируется стационарность режима работы. Процесс идет до тех пор, пока не будет найден вариант, удовлетворяющий заданному коэффициенту неравномерности хода.
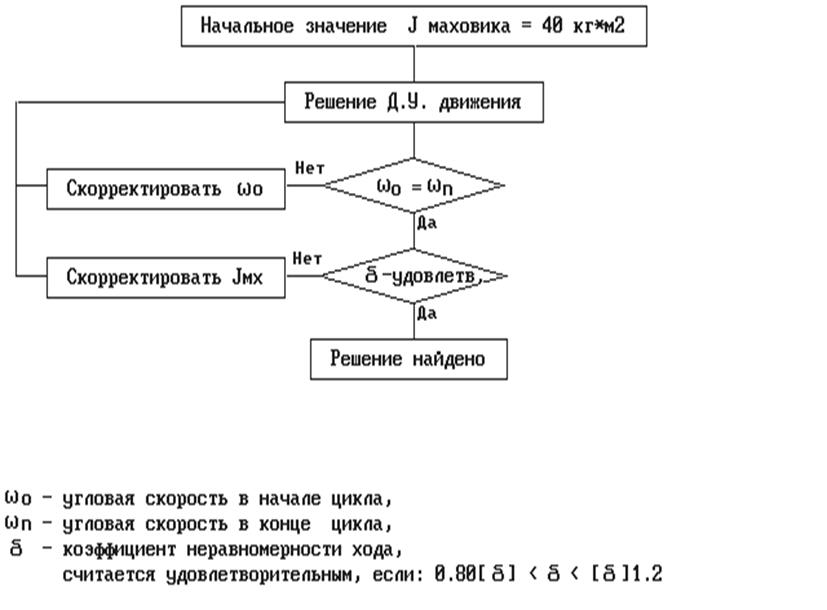
Рис. 8.1
8.2. Результаты математического моделирования и их анализ.
На рис. 8.1 Представлены результаты реализации описанного алгоритма. На рис. 8.2 В одну координатную сетку сведены все приведенные моменты, действующие на главные моменты, действующие на главный вал машины. На рис. 8.2 Функция скорости главного вала. На рис. 8.3 Функция ускорения главного вала.
Анализ этих зависимостей показывает:
1. Разгон и торможение главного вала обусловлены главным образом взаимодействием трех моментов Мдпр, Мспр и Мj
2. Максимальное значение момента Мдпр более чем в 2,5 раза меньше, чем у Мспр, следовательно технологическая операция производится главным образом за счет инерции маховика.
3. Влияние момента Мj заметно только на обратном ходе рабочего ползуна. Однако необходимо отметить, что если при конструктивной проработке главного рычажного механизма возникает необходимость в увеличении масс звеньев по сравнению с теми, которые были приняты в расчетах
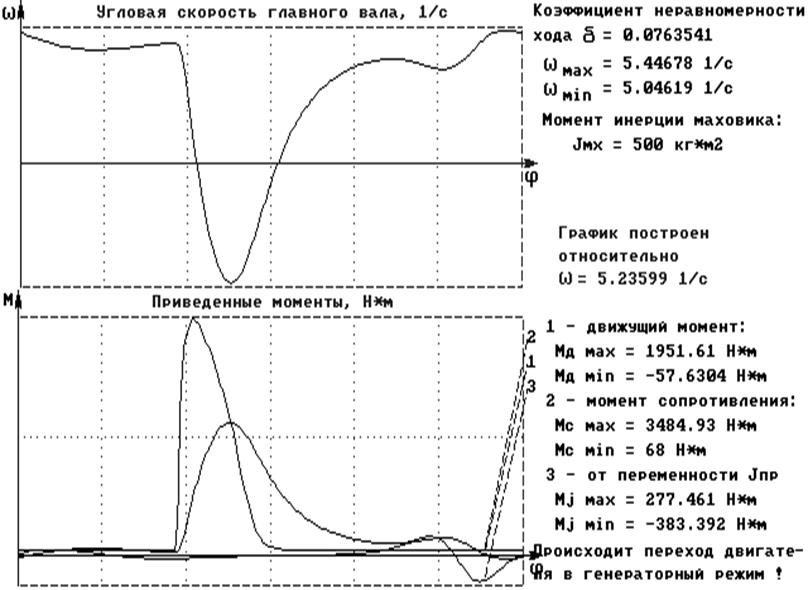
Рис. 8.2
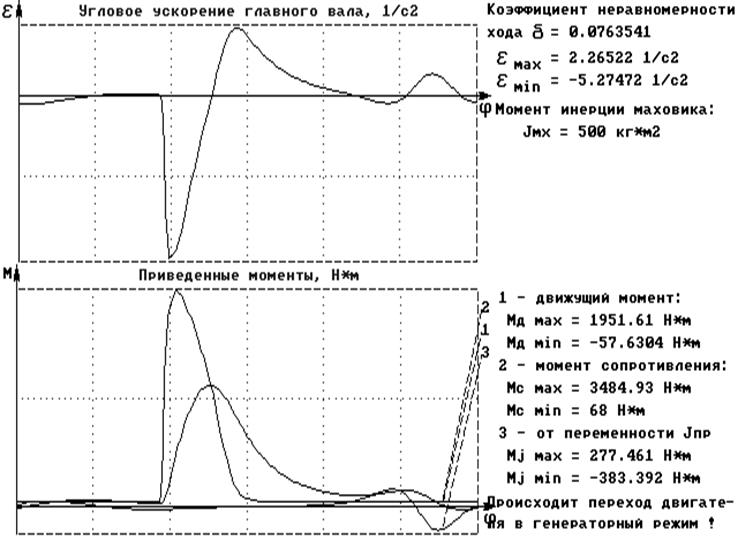
Рис. 8.3
данного проекта, то это может вызвать нежелательное увеличение внутренней виброактивности механизма..
Рассчитаем ориентировочные размеры маховика. Для этого можно приближенно предположить, что маховик представляет собой сплошной диск, момент инерции которого:
Jmx=pbπd4/32
Где, р – плотность материала (для стали и чугуна можно принять р=7800 кг/м3)
b, d, толщина и диаметр маховика.
Принимая для ориентировочно расчета b/d=5, имеем:
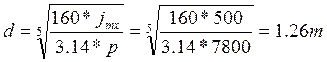
Конструктивно такой диаметр маховика слишком велик, однако обычно маховик изготавливают так, чтобы основная масса располагалась ближе к ободу, в этом случае диаметр заметно уменьшится, кроме того отношение b/d можно взять меньшим. Если установить маховик не на главный вал, а на вал двигателя, то его момент инерции:
J’mx=Jmx/i2=500/28,9*28,9=0,59 кг\м2, где i-передаточное отношение зубчатого механизма.
В этом случае диаметр маховика:
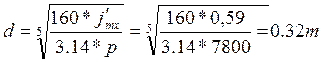
Причины изменения ω по каждому участку (рис. 8.5):
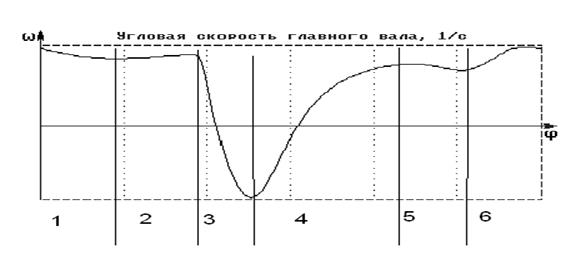
Рис. 8.5
Мд- движущий момент
Мс- момент сопротивления
Мj- момент от переменности Jпр
Участок 1: торможение главного вала
Мд < Мj +Мс
Мj - сопротивление
Участок 2: разгон главного вала
Мд >Мj +Мс
Мj - сопротивление
Мд +Мj > Мс
Мj - движущий
Участок 3: торможение главного вала
Мд +Мj < Мс
Мj - движущий
Участок 4: разгон главного вала
Мд +Мj > Мс
Мj - движущий
Мд >Мj +Мс
Мj - сопротивление
Участок 5: торможение главного вала
Мд <Мj +Мс
Мj - сопротивление
Участок 6: разгон главного вала
Мд >Мj +Мс
Мj - сопротивление
Мд +Мj < Мс
Мj - движущий
ЗАКЛЮЧЕНИЕ
В данном курсовом проекте решены следующие задачи:
- выполнен структурный анализ и кинематический синтез главного механизма с обеспечением требуемых параметров движения рабочего органа;
- произведен кинематический анализ работы главного механизма;
- определена требуемая мощность двигателя и выбран его тип;
- выбран тип зубчатого механизма для передачи движения с вала двигателя на вал кривошипа главного механизма произведено его кинематическое проектирование;
- произведен силовой расчет главного механизма с определением реакций в кинематических парах;
- исследована динамика работы машины м определены параметры маховика, обеспечивающего требуемую плавность хода.
ЛИТЕРАТУРА
1. Лавров В. Ю. Курсовое проектирование по ТММ и механике машин в среде пакета ТММ_КР. Учебное пособие. Санкт-Петербург, 1997 г.
2. Артоболевский И. И. Теория механизмов. Издательство «Наука», Москва, 1967 г.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.