Исследование и синтез машины – механического пресса (с механизмом подачи), страница 10

7.   70.00   8.6569e-001    34.44   7.1396e-001   4.8957e-001

8.   80.00   1.2293e+000    62.81   5.6178e-001   1.0934e+000

9.   90.00   1.6019e+000    76.42   3.7611e-001   1.5571e+000

10.  100.00   1.8800e+000    84.80   1.7046e-001   1.8723e+000

11.  110.00   2.0411e+000    91.16  -4.1157e-002   2.0406e+000

12.  120.00   2.0891e+000    96.74  -2.4526e-001   2.0747e+000

13.  130.00   2.0428e+000   102.16  -4.3014e-001   1.9970e+000

14.  140.00   1.9294e+000   107.72  -5.8728e-001   1.8378e+000

15.  150.00   1.7795e+000   113.60  -7.1243e-001   1.6307e+000

16.  160.00   1.6231e+000   119.78  -8.0609e-001   1.4088e+000

17.  170.00   1.4847e+000   126.02  -8.7310e-001   1.2009e+000

18.  180.00   1.3818e+000   131.82  -9.2139e-001   1.0298e+000

19.  190.00   1.3252e+000   136.46  -9.6060e-001   9.1284e-001

20.  200.00   1.3220e+000   139.19  -1.0006e+000   8.6407e-001

21.  210.00   1.3817e+000   139.47  -1.0502e+000   8.9788e-001

22.  220.00   1.5213e+000   137.22  -1.1166e+000   1.0332e+000

23.  230.00   1.7698e+000   132.84  -1.2035e+000   1.2977e+000

24.  240.00   2.1698e+000   127.09  -1.3084e+000   1.7309e+000

25.  250.00   2.7724e+000   120.74  -1.4170e+000   2.3829e+000

26.  260.00   3.6197e+000   114.33  -1.4914e+000   3.2981e+000

27.  270.00   4.6935e+000   108.05  -1.4540e+000   4.4626e+000

28.  280.00   5.7967e+000   101.67  -1.1720e+000   5.6770e+000

29.  290.00   6.3643e+000    94.35  -4.8294e-001   6.3459e+000

30.  300.00   5.4239e+000    82.95   6.6613e-001   5.3828e+000

31.  310.00   2.6876e+000    43.21   1.9588e+000   1.8402e+000

32.  320.00   4.4450e+000   -52.75   2.6907e+000  -3.5380e+000

33.  330.00   8.4074e+000   -73.16   2.4357e+000  -8.0468e+000

34.  340.00   9.8629e+000   -80.60   1.6110e+000  -9.7305e+000

35.  350.00   9.1105e+000   -84.28   9.0873e-001  -9.0651e+000

36.    0.00   7.4750e+000   -85.43   5.9539e-001  -7.4513e+000

Alf - ууюы яютю

Н  169.35 Ја. ®в ®бЁ Xo

3. ИНЕРЦИОННЫЕ ПАРАМЕТРЫ ГЛАВНОГО МЕХАНИЗМА

3.1. Массы и моменты инерции звеньев.

Для вычисления моментов инерции использовались следующие формулы:

J₁= 2,5*m₁*l²₁π/30

J_i= m_i*l²_iπ/30, i=2, 3, 4

где l_i  - длинна звена или его наибольший размер.

Эмпирический коэффициент 2,5 в формуле момента инерции кривошипа учитывает дополнительные массы при его уравновешивании.

Значения масс звеньев и их моменты инерции указаны в таблице №1

Таблица № 1

3.2. Приведение масс и моментов инерции.

Приведенный момент инерции характеризует инерционные свойства механизма так, что величина J_прω²₁/2 в каждый момент времени есть кинетическая энергия, которой суммарно обладают все звенья механизма. Поскольку шарнирно-рычажный механизм в процессе движения меняет свою конфигурацию, величина приведенного момента инерции меняется и является функцией положения, в данном случае – угла поворота кривошипа.

Функция J_пр(φ₁) вычисляется для каждого положения механизма по формуле:

J_пр(φ₁) =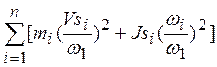

Эта формула получена из условия равенства кинетических энергий механизма и звена приведения, т.е. приведенный момент инерции является мерой инертности всего механизма.

Для расчетного положения:

J_пр(φ₁)= J₁ + m₂(V_S2/ω₁)² + J₂(ω₂/ ω₁)² + m₃(V_S3/ω₁)² + J₃(ω₃/ ω₁)² + m₄(V_S4/ω₁)² + J₄(ω₄/ ω₁)² + m₅(V₅/ω₁)² = 7,765  кг*м²

На рис. 3.1  приведен график приведенного момента инерции за цикл:

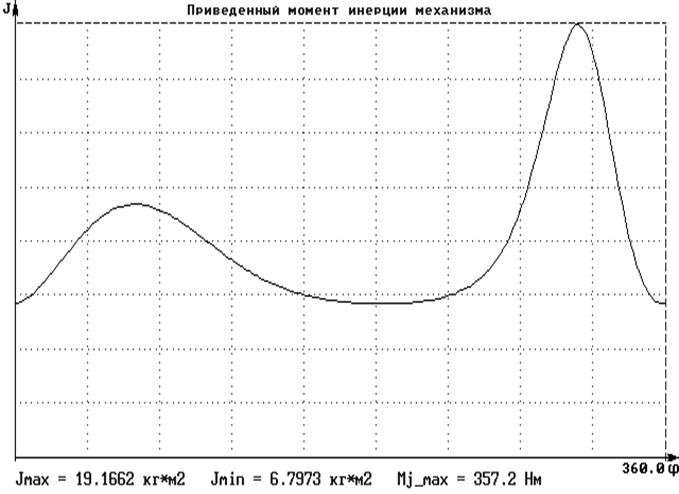
Рис. 3.1

4. ВНЕШНЯЯ НАГРУЗКА

По заданию на рабочем участке хода ползуна действует технологическая сила F_T = 44 кН рис. 4.1. Рабочий участок располагается на прямом ходе ползуна, когда он движется сверху вниз. Величина рабочего хода: S_p=0,25 S_п.

где  S_п – полный ход рабочего ползуна.

S_p=0,25*0.28=0.07 м

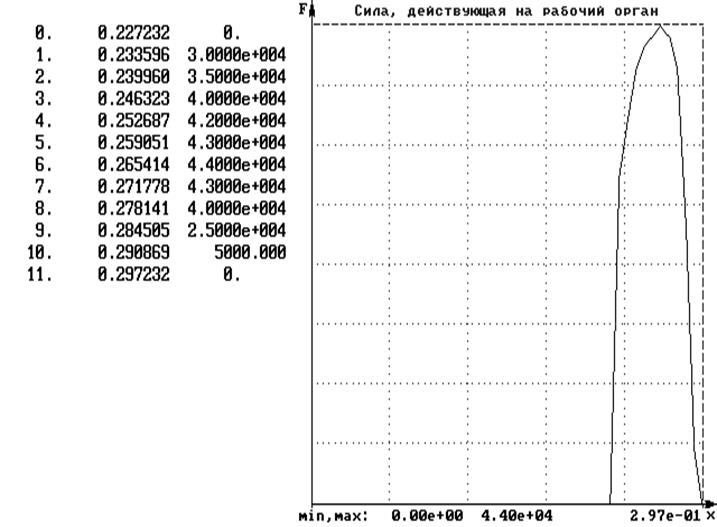
Рис. 4.1