В массиве выборки seed хранятся: значение случайных величин, число повторений случайной величины в выборке, её функция распределения. Для вычисления бета и гамма распределений используются стандартные модули.
2.5. Алгоритм формирования массива статистик Колмогорова
Входные данные – выборка случайных чисел, подчиняющихся заданному закону распределения.
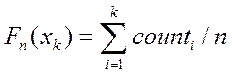 |
n – объём выборки.
Шаг2. Вычисляется Dn – максимальная разность эмпирической функции распределения от теоретической.
Шаг3. Вычисляется статистика Колмогорова по формуле
![]()
Sk = (6nDn + 1)/ 6
и эта величина заносится в массив статистик.
Отметим, что выборки хранятся по одной, т.е. первая сгенерированная по заданному закону распределения выборка хранится в массиве seed, по этой выборке вычисляется статистика Колмогорова, которая записывается в массив stat, после чего производится очистка массива выборок. Затем в seedзаписывается вторая сгенерированная выборка, для которой также вычисляется статистика Колмогорова и т.д.
Сформированная выборка статистик Колмогорова сохраняется в файл *.dat в виде
<название распределения>, <генератор>, <параметры распределения>, <число элементов в выборке распределения>, <число выборок распределения>, <статистика>
0 <число выборок распределения>
<значение1>
<значение2>
…
<значениеN>
Очевидно, что число элементов в массиве статистик N равно числу выборок распределений.
2.6. Алгоритм проверки гипотезы о согласии с равномерным на [0, 1] распределением по критерию согласия хи-квадрат
Шаг1. С помощью выбранного генератора генерируется случайное число.
Шаг2. Сгенерированная случайная величина добавляется в массив выборки. Выборка разбивается на некоторое число интервалов, каждому интервалу выборки соответствует величина count – сколько элементов попало в интервал. Если новая сгенерированная случайная величина уже присутствует в выборке, то count соответствующего интервала увеличивается на 1, иначе новая случайная величина добавляется в массив и её count = 1.
Шаг3. Выборка сортируется по возрастанию значений её элементов.
Шаг4. Вычисляется статистика критерия и её значение сравнивается с табличным значением. Если вычисленная статистика меньше табличной, то значит сгенерированная выборка действительно равномерна на [0, 1].
2.7. Экранные формы диалогов пользователя
При запуске программы, генерирующей выборку статистик Колмогорова, появляется экранная форма, содержащая информацию об используемом генераторе, законе распределения, параметрах распределения, количестве элементов в выборке и количестве выборок. Вся эта информация может варьироваться. Экранная форма для геометрического распределения представлена на рисунке 2.1, для биномиального распределения - на рисунке 2.2, для распределения Пуассона - на рисунке 2.3.
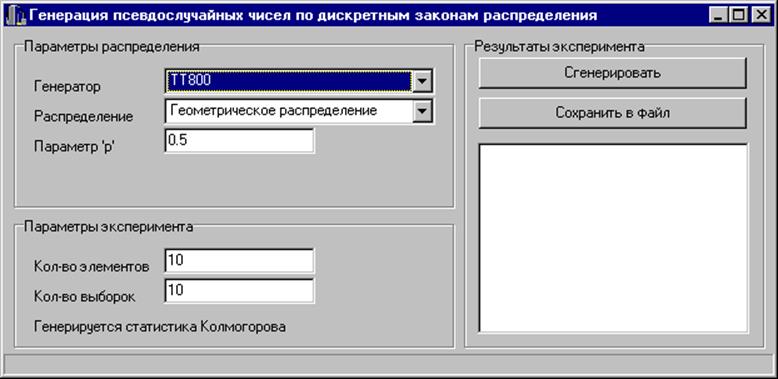
Рис. 2.1. Экранная форма для геометрического распределения
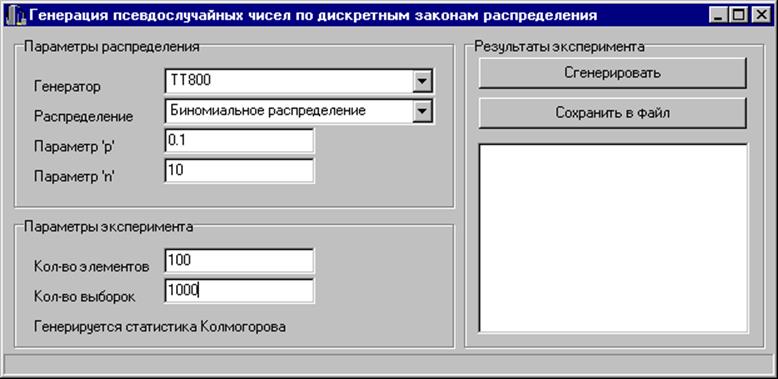
Рис. 2.2. Экранная форма для биномиального распределения
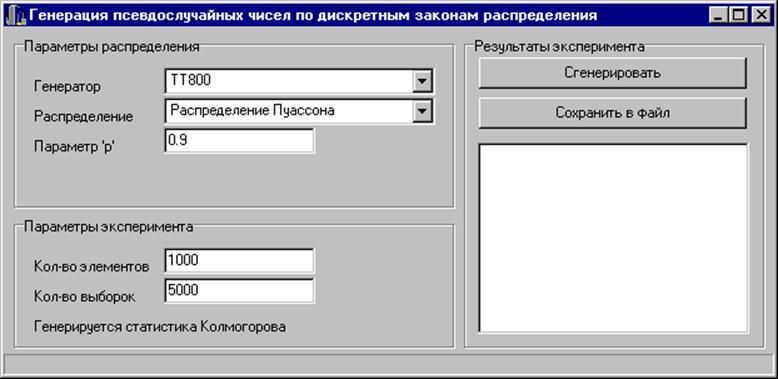
Рис. 2.3. Экранная форма для распределения Пуассона
Дадим некоторые пояснения. Поле “генератор”: выбирается генератор равномерно распределённых на [0, 1] случайных величин (Mersenne Twister или TT800). Поле “распределение”: выбирается дискретный закон распределения (геометрическое, биномиальное, Пуассона). Для геометрического распределения поле “параметр ‘ p’ ”: вероятность выпадения первого успеха, может принимать значения от 0 до 1. Для биномиального распределения поле “параметр ‘ p’ ”: вероятность появления события в каждом испытании , может принимать значения от 0 до 1; поле “параметр ‘ n’ ”: количество независимых испытаний, любое целое положительное число. Для распределения Пуассона поле “параметр’ p’”: любое положительное число. Поле “кол-во элементов”: количество элементов в выборке случайных чисел, сгенерированных по выбранному закону распределения. Поле “кол-во выборок”: количество выборок случайных чисел, сгенерированных по выбранному закону распределения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.