Исследование Законов распределения. Статистики Колиогорова, страница 3

Пусть X = (X₁, ,.., Х_n) — выборка объема n из распределения L(x) и x = (x₁, ..., x_n) — наблюдавшееся значение X. Каждой реализации х выборки X можно поставить в соответствие упорядоченную последовательность [4]

x₍₁₎<=x₍₂₎<=…<=x_(n)                                                         (1.1)

где   x₍₁₎=min(x₁,  ...,x_n),  x₍₂₎ — второе   по   величине значение среди x_1,…, x_nи т. д., x_(n) = max(x_1,…, x_n).

Обозначим через X_(k) случайную величину, которая для каждой реализации х выборки X принимает значение x_(k), k = 1, ..., n. Так по выборке X определяют новую последовательность случайных величин Х₍₁₎, ..., Х_(n), называемых порядковыми статистиками выборки [4]; при этом Х_(k]—k-я порядковая статистика, а X₍₁₎, и X_(n) — экстремальные значения выборки. Из определения порядковых статистик следует, что они удовлетворяют неравенствам

X₍₁₎<=X₍₂₎<=…<=X_(n)                                          (1.2)

Эту последовательность  называют вариационным рядом выборки.

Симметричные относительно концов элементы последовательности Х_(m) и      Х_(n-m+1) иногда называют соответственно m-м наименьшим и m-м наибольшим значениями выборки (m=1, 2, ...); при m= 1 получаем экстремальные значения выборки. Итак, вариационный ряд— это расположенные в порядке возрастания их величин элементы выборки. Отметим, что для заданной реализации x = (x₁, ..., x_n) выборки  X = (X₁, ,.., Х_n) реализацией последовательности (1.2) является последовательность (1.1).

1.3. Эмпирическая функция распределения

Определим для каждого действительного х случайную величину m_n(х), равную числу элементов выборки Х = (Х₁ ..., Xn) [5], значения которых не превосходят х, т. е.

m_n(х)= |{j:X_j<=x}|

где через |А| обозначено число элементов конечного множества А, и положим F_n(x)= m_n(х)/n. Функция F_n(x) называется эмпирической функцией распределения (соответствующей выборке X) [5]. Функцию распределения F{x) наблюдаемой случайной величины x в этом случае называют иногда теоретической функцией распределения.

По своему определению эмпирическая функция распределения — случайная функция: для каждого х Î R значение F_n (х) — случайная величина, реализациями которой являются числа 0, 1/n, 2/n, ..., {n — 1)/n, n/n = 1, и при этом

P (F_n(x) = k/n) = P (m_n(х)=k).

Но  из  определения  m_n(х) следует,   что L (m_n(х)) = Bi (n, р), где р = Р (x<=х) = F (х). Поэтому

P (F_n(x) = k/n) = Cⁿ_k F^k(x)(1-F(x))^n-k,   k = 0, 1, ..., n.

Итак, эмпирическая функция распределения (как и вариационный ряд)— некоторая сводная характеристика выборки. Для каждой реализации х выборки X функция F_n(x) однозначно определена и обладает всеми свойствами функции распределения: изменяется от 0 до 1, не убывает к непрерывна справа. При этом она кусочно-постоянна и возрастает только в точках последовательности (1.1). Если все компоненты вектора х различны (в последовательности (1.1) все неравенства строгие), то функция F_n(x) задается [5], очевидно, соотношениями

                                  

0    при x<x₍₁₎,

F_n(x) =       k/n при x_(k) ≤ x ≤  x_(k+1),

1 при x ≥ x_(n),

т. е. в этом случае величина всех скачков равна 1 /n. В общем случае эмпирическую функцию распределения можно записать в виде

F_n(x) = 1/n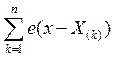                   (1.3)

где   е(х) — функция   единичного   скачка  [6] (функция   Хевисайда):                     

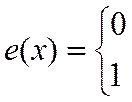 при  x<0,  при  x>=0.

В представлении   (1.3) хорошо видна зависимость F_n(x) от выборки X.

Эмпирическая функция распределения играет фундаментальную роль в математической статистике. Важнейшее её свойство состоит в том, что при увеличении числа испытаний над случайной величиной x происходит сближение этой функций с теоретической.

Таким образом, если объем, выборки большой, то значение эмпирической функции распределения в каждой точке х может служить приближенным значением (оценкой) теоретической функции распределения в этой точке. Функцию F_n(x) часто называют в этом случае статистическим аналогом для F (х).

1.4.  Проверка гипотез о виде распределения