Исследование Законов распределения. Статистики Колиогорова, страница 4

Статистической гипотезой [7] называется любое утверждение о виде или свойствах распределений наблюдаемых в эксперименте случайных величин.

Проверка статистической гипотезы состоит в том, чтобы сформулировать такое правило, которое позволяло бы по результатам соответствующих наблюдений принять или отклонить гипотезу.

Правило, согласно которому гипотеза принимается или отвергается, называется критерием проверки гипотезы [7].

Если гипотеза Н₀ однозначно фиксирует распределение наблюдений, то она называется простой гипотезой, иначе – сложной.

Существуют следующие виды статистических гипотез:

1.  гипотеза о виде распределения

2.  гипотеза однородности

3.  гипотеза независимости

4.  гипотеза случайности

В рамках данной работы нас будут интересовать только простые гипотезы о виде распределения. Пусть Х = (Х₁, … , Х_n) – выборка из некоторого распределения с неизвестной функцией распределения F_ξ(х), о которой выдвинута простая гипотеза Н₀: F_ξ(х) = F(х).

Итак, пусть о распределении случайной величины ξ сформулирована гипотеза Н₀. Алгоритм построения критерия проверки этой гипотезы [8] состоит в следующем:

·  находим статистику Т = Т (Х_n), характеризующую отклонение эмпирических данных от гипотетических данных.

·  Находим распределение этой статистики при условии истинности гипотезы Н₀: {G_T (x)| H₀}.

·  Правило проверки гипотезы Н₀ можно сформулировать следующим образом: если

P{T > T(X_n)} = 1 - {G_T (x)| H₀} < α,   

          где T(X_n) – значение статистики, вычисленное по выборке,

                       α – уровень значимости критерия,

         то гипотеза  отвергается как противоречащая статистическим данным.     

         Иначе, если

                    P{T > T(X_n)} = 1 - {G_T (x)| H₀} > α

         то нет оснований отказываться от выдвинутой гипотезы и следует

         считать, что наблюдение не противоречит гипотезе Н₀.

Обычно статистика критерия является неотрицательной [10], т.к. является расстоянием между теоретическим и эмпирическим распределением, поэтому функция распределения начинается с нуля.

Статистику Т(Х_n) называют статистикой критерия.

Уровень значимости α характеризует вероятность ложного отвержения гипотезы Н₀, когда она верна.

1.5.  Критерий согласия  Колмогорова

Одним из наиболее известных критериев проверки этой гипотезы [11] является критерий согласия Колмогорова. Его применяют в тех случаях, когда функция F(х) непрерывна.

Колмогоровым было получено распределение статистики [11]

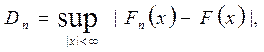                                                                                           (1.5)

представляющей собой  максимальное отклонение эмпирической функции распределения F_n(х) от гипотетической  функции распределения F_n(х) (функции закона распределения, согласие с которым проверяется). При каждом х величина F_n(х) является оптимальной оценкой для F(х) и с увеличением объёма выборки n происходит сближение F_n(х) с F(х), поэтому, по крайней мере при больших n, в тех случаях, когда гипотеза Н₀ истина, значение D_n не должно существенно отклоняться от нуля. При n → ∞ распределение статистики         сходится равномерно к распределению Колмогорова [11]

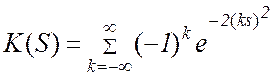                                             (1.6)

Статистика критерия Колмогорова имеет  вид [12]

                                     S_k = (6nD_n + 1)/ 6           (1.7)

Распределение величины S_k при простой гипотезе в пределе подчиняется закону Колмогорова K(S).

Гипотеза согласия отклоняется, когда

P{S > S_k^*} = 1 – K(S_k^*) < α,     (1.8)

Где S_k^* - значение статистики, вычисленное по выборке.

1.6. Критерий согласия Колмогорова для дискретных распределений

Определим критерий Колмогорова для дискретных распределений. Нами выдвинуто предположение, что критерий Колмогорова для проверки простой гипотезы о виде распределения Н₀: F_ξ(х) = F(х) можно применять также и в том случае, когда функция F(х) – дискретна. В этом случае мы будем рассматривать статистику критерия в следующем виде [12]: