Исследование Законов распределения. Статистики Колиогорова, страница 12

Изменение величин сдвига и масштаба логнормльного распределения при изменении параметра  биномиального распределения  n

Из данной таблицы видна следующая закономерность: при увеличении значения параметра n  величина масштаба логнормального распределения уменьшается,  величина сдвига увеличивается. Причём уже при n≥500 величина масштаба  одинакова. Зависимость сдвига логнормального распределения от параметра n биномиального распределения довольно хорошо аппроксимируется логарифмической зависимостью, что показано на рисунке 3.16.

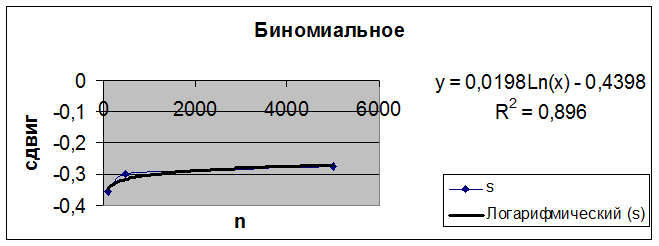
Рис.3.16. Аппроксимация зависимости сдвига от параметра n

Таким образом, величина сдвига s может быть найдена через уравнение

s = 0.0198Ln(n) – 0.4398.

Зависимость масштаба от параметра n аппроксимировать не удалось.

В таблице 3.5 представлены уравнения зависимости масштаба и сдвига логарифмически нормального распределения от параметров дискретных распределений.

                                                                                                        Таблица 3.5.

Зависимость величин  масштаба и сдвига от значения параметров

3.5. Выводы

В третьей главе данной  работы представлены результаты тестирования полученных выборок с помощью программы «Статистический анализ одномерных интервальных наблюдений». Сгенерированные выборки статистик Колмогорова для дискретных законов распределения проверяются на согласие с

·  законом распределения Колмогорова. По результатам моделирования хорошее согласие ни в одном тесте не достигалось;

·  логарифмически нормальным законом. По результатам моделирования получилось хорошее согласие во всех тестах для любых параметров всех дискретных законов по критериям согласия хи-квадрат и отношения правдоподобия (по остальным критериям гипотеза отвергалась, что связано с дискретностью полученных статистик). Также найдены законы изменения величин масштаба и сдвига логнормального распределения в зависимости от значения параметров дискретных распределений.

ЗАКЛЮЧЕНИЕ

Итак, подведём итоги.     В ходе бакалаврской работы были изучены основные понятия, необходимые для проверки гипотез о согласии эмпирической выборки с теоретическим законом распределения, выбрано несколько дискретных распределений. Реализованы в программе алгоритмы генерации выборки по заданному закону распределения, алгоритм генерации выборки статистик Колмогорова для дискретных распределений. Данная работа содержит тесты, которые позволяют провести необходимые исследования влияния факторов на закон распределения статистик Колмогорова, а также отражают правильность работы программы.

В ходе выполнения работы мы пришли к выводу, что распределение статистик Колмогорова для дискретных законов распределения не совпадает с распределением Колмогорова, хотя и близко к нему в редких случаях при наложении определённых ограничений на параметры распределений. Так, например, распределение статистик Колмогорова для геометрического распределения близко к  распределению Колмогорова при маленьких значениях параметра р, для распределения Пуассона – при больших  значениях параметра р и , наконец, для биномиального распределения – при р = 0.5 и больших значениях параметра n.