Исследование Законов распределения. Статистики Колиогорова, страница 11

а). Сравним с распределением Колмогорова. Выявлена следующая закономерность: при увеличении значения параметра р от 0 до 0.5 включительно распределение выборки, сформированной из статистик Колмогорова, приближается к распределению Колмогорова, а при изменении значения р от 0.5 до 1 оно опять отклоняется от желаемого распределения. Причём по графикам видно, отклонение от распределения Колмогорова симметрично приближения к нему, что, вероятно связно с симметричностью хвостов биномиального распределения. Таким образом, наилучший результат достигается при р = 0.5, но всё-таки хорошее согласие не достигается. Вид распределений представлен на рисунке 3.11.

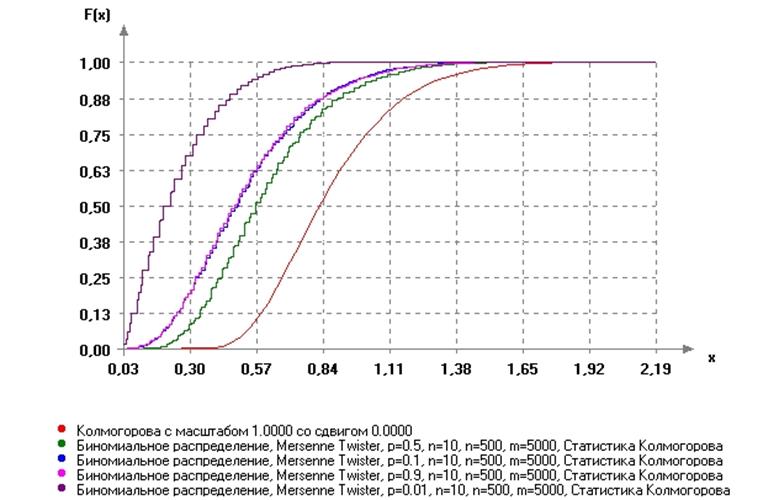
Рис.3.11. Вид распределений статистик Колмогорова для биномиального

распределения  при разных значениях параметра р

б). Сравним с логарифмически нормальным законом. При всех значениях параметра р выборка статистик Колмогорова достаточно хорошо подчиняется логнормальном закону распределения с разными значениями масштаба и сдвига, но наилучшее согласие достигается при р=0.5, что хорошо видно, например, на рисунке 3.12.

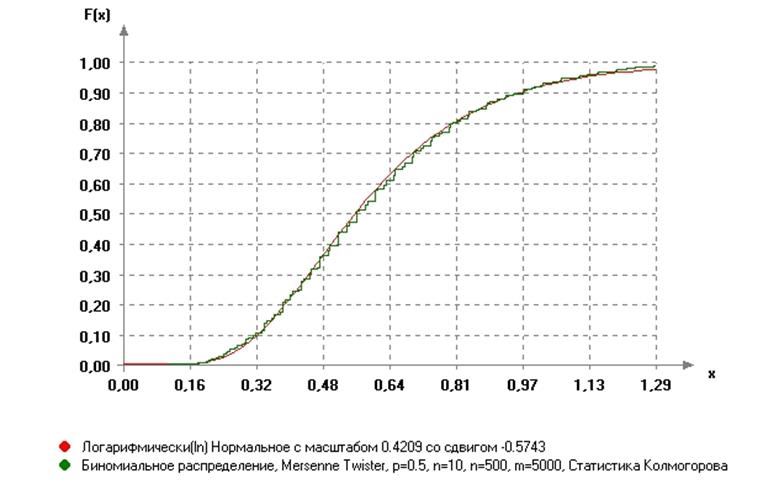
Рис.3.12. Вид распределения статистик Колмогорова для биномиального закона при р=0.5  по отношению к логнормальрому распределению

Изменение величин сдвига и масштаба логнормльного распределения при изменении параметра р биномиального распределения представлено в таблице 3.3.

                                                                                                                Таблица 3.3.

Изменение величин сдвига и масштаба логнормльного распределения при изменении параметра  биномиального распределения  р

Значение параметра р	Масштаб	Сдвиг
0.9	0.5300	-0.7654
0.5	0.4209	-0.5743
0.1	0.5241	-0.7570
0.01	0.7897	-1.6529

Из данной таблицы видна следующая закономерность: при увеличении значения параметра р до 0.5 величина масштаба логнормального распределения уменьшается,  величина сдвига увеличивается, а при дальнейшем увеличении параметра р масштаб увеличивается, сдвиг уменьшается. Причём при симметричных относительно р=0.5 значениях параметра величины масштаба и сдвига практически одинаковы. Зависимость масштаба логнормального распределения от параметра р биномиального распределения довольно хорошо аппроксимируется квадратичной параболой, что показано на рисунке 3.13.

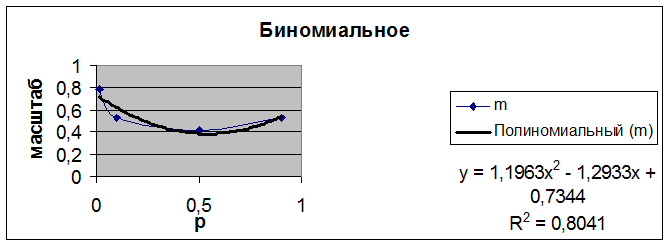
Рис.3.13. Аппроксимация зависимости сдвига от параметра р

Таким образом, величина масштаба m может быть найдена через уравнение

m = 1.1963р² – 1.2933р + 0.7344.

Зависимость сдвига от параметра р аппроксимировать не удалось.

3). Варьируется величина параметра n при постоянстве остальных факторов:

p = 0.5, количество элементов = 100, количество выборок = 5000,

n = (100, 500, 5000).

а). Сравним с распределением Колмогорова. Выявлена следующая закономерность: при увеличении значения параметра n распределение выборки, сформированной из статистик Колмогорова, приближается к распределению Колмогорова, однако хорошее согласие не достигается и уже при n > 500 (даже если n намного больше 500), вид распределения практически не меняется. Вид распределений представлен на рисунке 3.14.

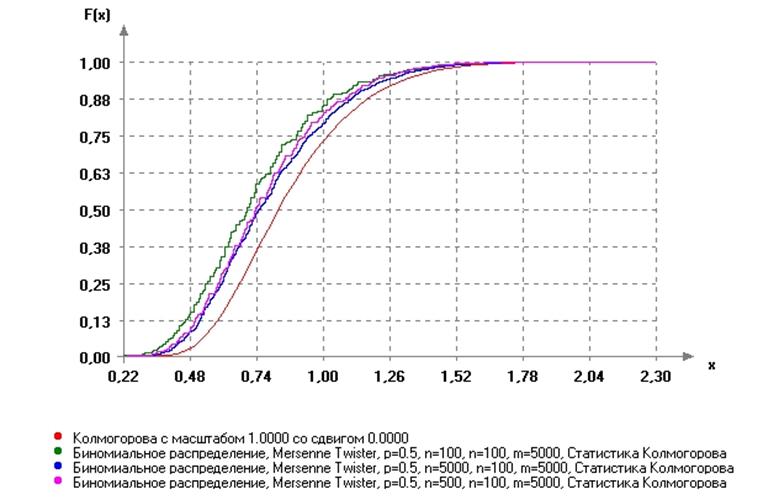
Рис.3.14. Вид распределений статистик Колмогорова для биномиального

распределения  при разных значениях параметра n

б). При всех значениях параметра n выборка статистик Колмогорова хорошо подчиняется логнормальном закону распределения с разными значениями масштаба и сдвига,  что хорошо видно, например, на рисунке 3.15.

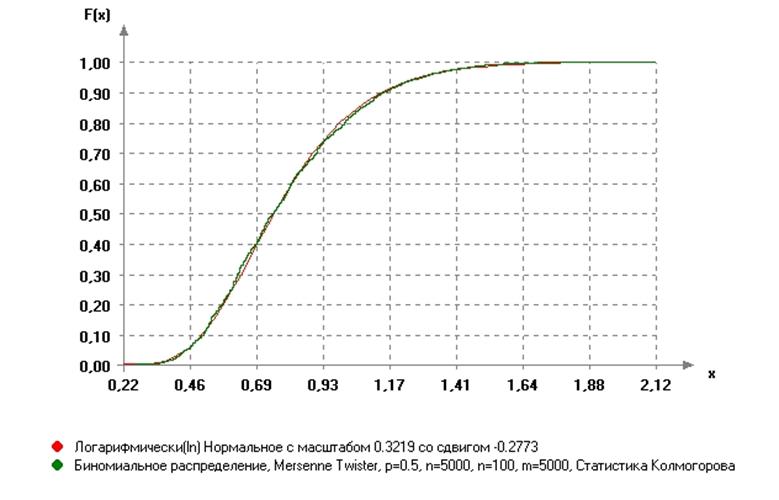
Рис.3.15. Вид распределения статистик Колмогорова для биномиального закона при n=5000  по отношению к логнормальрому распределению

Изменение величин сдвига и масштаба логнормльного распределения при изменении параметра n биномиального распределения представлено в таблице 3.4.

                                                                                                                Таблица 3.4.