Исследование Законов распределения. Статистики Колиогорова, страница 2

Вероятностным пространством [1]называется (Ω,А,Р), где Ω={ω} – непустое множество, называемое пространством элементарных событий (элементы ω интегрируются как взаимно исключающие исходы изучаемого случайного явления); А – некоторая выделенная совокупность подмножеств множества Ω , называемых событиями ; Р – вероятность, заданная на событиях АÎА.

Пространство  называется дискретным [1], если количество его элементов конечно или счетное, в противном случае оно называется непрерывным.

Рассмотрим некоторое множество - дискретное, и некоторую случайную величину , заданную на вероятностном пространстве 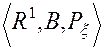, такую что

.

Тогда  называется дискретной случайной величиной [1]. Другими словами, дискретная случайная величина-это случайная величина, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

          Для дискретной случайной величины недостаточно перечислить все возможные ее значения, нужно еще указать их вероятности.

Законом распределения дискретной случайной величины [1] называют соответствие между возможными значениями и их вероятностями.

Для дискретных случайных величин имеет место ряд распределения вероятностей.

          Множество дискретных распределений, которое будет использовано для реализации в системе [2], описано ниже.

1). Биномиальное распределение Bi (k| n, p).

P{ξ(ω)=k}=C_n^kp^k(1-p)^n-k ,  0≤р≤1, 0≤k≤n

ξ(ω)=0,1,…,n

Проводится случайный эксперимент, состоящий из n-серий независимых испытаний. В каждом испытании фиксируется, появилось событие А или нет. Событие А появляется с вероятностью р, а вероятность не появления равна (1-р); ξ(ω) – количество успешных испытаний.

Отметим важное свойство: функции биномиального и бета распределений связаны следующим соотношением

Bi (k| n, p) = B (1-p| n-k, k+1) .

Связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.

2). Геометрическое распределение G(k| р).

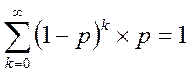
P{ξ(ω)=k}=р(1-р)^k , 0≤р≤1,  k≥1,

     ξ(ω)=1,…,k

Проводят независимые эксперименты с двумя исходами. Эксперимент завершается, когда первый раз наблюдается успех; ξ(ω) – число испытаний до выпадения первого успеха.

3). Распределение Пуассона Р₀(k| λ).

P{ξ(ω)=k}=е^-λ λ/ k! , λ>0,

ξ(ω)=0,1,2,…

Отметим важное свойство: функции распределения Пуассона и гамма распределений связаны следующим соотношением

P₀ (k| λ) = Г (k+1| λ).

Поэтому при вычислении функции распределения следует воспользоваться упомянутой связью пуассоновского и гамма-распределения.

Введём немного информации о бета (Таблица 1.1.) и гамма (Таблица 2.1.) распределениях [3].                                                                                                       

Таблица 1.1.

Основные характеристики бета-функции

Обозначение
Область значений:
Параметры	Параметры формы: a,b > 0.
Плотность функции распределения	, где – (полная) бетафункция от параметров a и b.

 Таблица2.2.

Основные характеристики гамма-функции

Обозначение
Область значений
Параметры	Параметр формы a > 0
Плотность функции распределения	, где – (полная) гамма-функция от параметра a.

Гамма-функция, задаваемая соотношением [3]

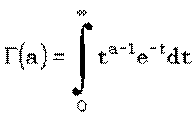
входит в нормирующий множитель практически во все функции распределения. Поэтому, естественно, важно уметь ее вычислять. Трудность, однако, в том, что эта функция очень быстро растет [3]: ведь для нее выполнено соотношение

, т.е. для целых аргументов она растет как факториал, и не медленнее для дробных.

Бета-функция вычисляется через гамма-функцию [3] следующим образом

B(a, b) = Г(a)Г(b)/Г(a+b).

Введём ещё несколько понятий.

1.2.  Порядковые статистики и вариационный ряд выборки