Исследование Законов распределения. Статистики Колиогорова, страница 10

Таким образом, величина сдвига s может быть найдена через уравнение

s = 0.6794p³ + 0.4469p² – 1.3745p – 0.2111.

3.3. Распределение статистик Колмогорова для распределения                  Пуассона

Случайная величина подчиняется закону распределения Пуассона Р₀(p). 1). Варьируется количество элементов в выборке, элементы которой распределены по пуассоновскому закону, при постоянстве остальных факторов:

р = 0.9, количество выборок = 5000, количество элементов = (10, 100, 500, 1000).

Выявлена следующая закономерность: количество элементов не влияет на распределение, но при его уменьшении увеличивается дискретность наблюдения. Вид распределений представлен на рисунке 3.6.

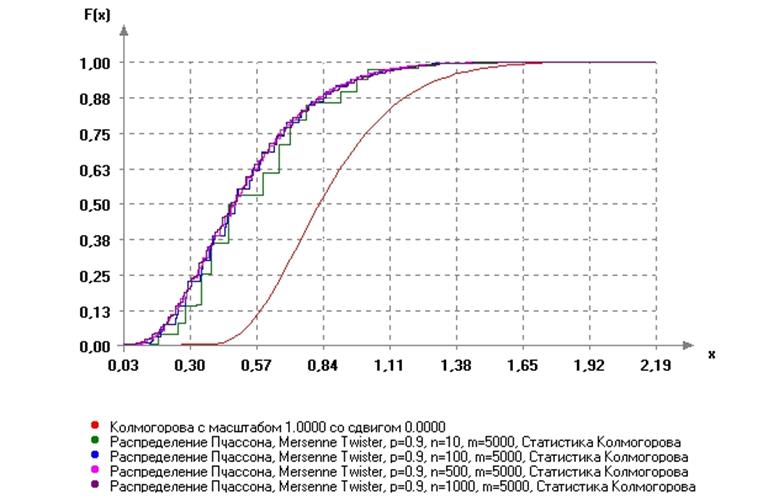
Рис.3.6. Вид распределений статистик Колмогорова для распределения

Пуассона  при разном количестве элементов в выборке   распределения

2). Варьируется величина параметра  р при постоянстве остальных факторов:

количество элементов = 500, количество выборок = 5000, р = (100, 500, 1000, 5000).

а). Сравним с распределением Колмогорова. Выявлена следующая закономерность: при увеличении значения параметра р распределение выборки, сформированной из статистик Колмогорова, приближается к распределению Колмогорова, однако хорошее согласие не достигается. Вид распределений представлен на рисунке 3.7.

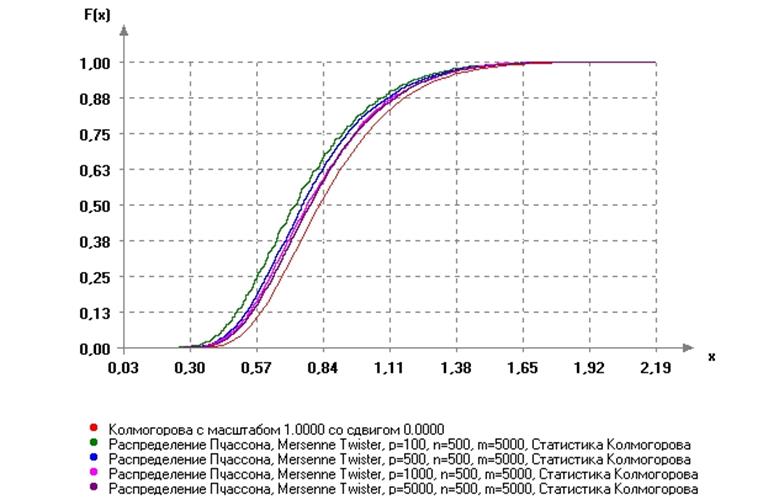
Рис.3.7. Вид распределений статистик Колмогорова для распределения

Пуассона при разных значениях параметра р

б). Сравним с логарифмически нормальным законом. При всех значениях параметра р выборка статистик Колмогорова хорошо подчиняется логнормальном закону распределения с разными значениями масштаба и сдвига, что хорошо видно, например, на рисунке 3.8.

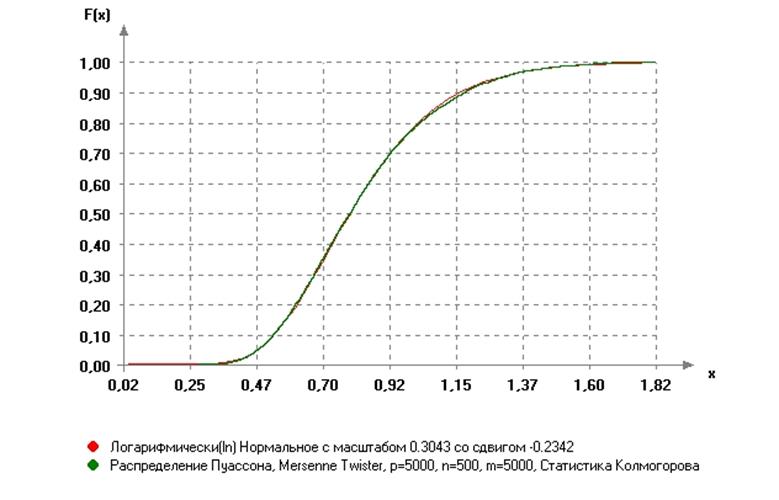
Рис.3.8. Вид распределения статистик Колмогорова для пуассоновского закона при р=5000  по отношению к логнормальрому распределению

Изменение величин сдвига и масштаба логнормльного распределения при изменении параметра  распределения Пуассона  представлено в таблице 3.2.

                                                                                                                Таблица 3.2.

Изменение величин сдвига и масштаба логнормльного распределения при изменении параметра  распределения Пуассона р

Значение параметра р	Масштаб	Сдвиг
100	0.3333	-0.3163
500	0.3116	-0.2710
1000	0.3099	-0.2465
5000	0.3043	-0.2342

Из данной таблицы видна следующая закономерность: при увеличении значения параметра р величина масштаба логнормального распределения уменьшается,  величина сдвига увеличивается. Зависимость сдвига логнормального распределения от параметра р распределения Пуассона довольно хорошо аппроксимируется логарифмической зависимостью, что показано на рисунке 3.9.

Рис.3.9. Аппроксимация зависимости сдвига от параметра р

Таким образом, величина сдвига s может быть найдена через уравнение

s = 0.0214Ln(p) – 0.4076.

Зависимость масштаба от параметра р аппроксимировать не удалось.

3.4. Распределение статистик Колмогорова для биномиального распределения

Случайная величина подчиняется биномиальному закону распределения Bi(n, p).

1). Варьируется количество элементов в выборке, элементы которой распределены по биномиальному закону, при постоянстве остальных факторов:

р = 0.5,

n = 100, количество выборок = 5000, количество элементов = (10, 100, 500, 1000).

Выявлена следующая закономерность: количество элементов не влияет на распределение, но при его уменьшении увеличивается дискретность наблюдения. Вид распределений представлен на рисунке 3.10.

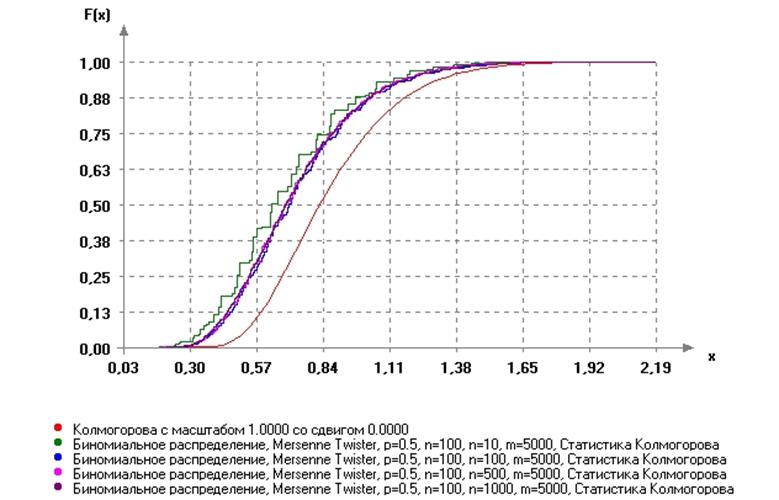
Рис.3.10. Вид распределений статистик Колмогорова для биномиального

распределения   при разном количестве элементов в выборке

распределения

2). Варьируется величина параметра  р при постоянстве остальных факторов:

n = 10, количество элементов = 500, количество выборок = 5000, р = (0.01, 0.1, 0.5, 0.9).