Исследование Законов распределения. Статистики Колиогорова, страница 5

                       S_k = (6nD_n + 1)/ 6   ,                       (1.9)

где D_n = 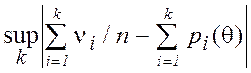.                      (1.10)

Здесь ν_i – число повторений i-го элемента выборки случайных чисел,

           n – объём выборки,

           р_i  - вероятность выпадания i-го элемента выборки.

Для того, чтобы определить распределение статистики (1.9), необходимо сделать следующее:

1.  Для заданного параметра выбранного распределения сгенерировать большое число выборок.

2.  Вычислить для сгенерированных выборок статистики Колмогорова по формуле (1.9).

3.  Идентифицировать распределение G(S_k| H₀).

Если статистика Колмогорова подчиняется распределению (1.6), то данный критерий можно использовать без изменений. Иначе надо установить множество законов распределения, которым подчиняется статистика (1.9) при изменении вида дискретного распределения, объёма выборки и значений параметров.

1.7. Критерий согласия хи-квадрат Пирсона

На практике вычисление статистики D_n – трудоёмкая задача, поэтому часто применяют другой критерий [13], называемый критерием χ². Его можно использовать для любых распределений, в том числе и многомерных. Чтобы воспользоваться этим критерием, выборочные данные предварительно группируют, т.е. переходят к частному представлению исходных данных. Пусть ν = (ν₁, …,ν_N) – вектор частот попадания выборочных точек в соответствующие интервалы группировки Е₁, …, Е_N  (ν₁+…+ ν_N = n) и р⁰=(р⁰₁,…, р⁰_N), где р⁰_j = P(ξ € Е_j| H₀), j = 1,…,N. В этом случае гипотеза Н₀ сводится к гипотезе о том, что вероятности полиномиального распределения построенного вектора частот ν имеют заданные значения р⁰_j, j=1,…,N. В качестве статистики, характеризующей отклонение выборочных данных (т.е. частот ν_j) от соответствующих гипотетических значений  (в данном случае от средних Е(ν_j| H₀) = np⁰_j), принимают величину [13]

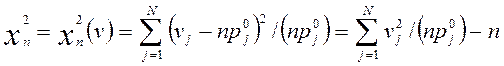
(1.11)

а критическую область задают в виде Г_1α = {t ≥ t_α}. Точное распределение L(X²_n| H₀) неудобно для вычисления (при заданном уровне значимости) критической границы t_α, но для больших объёмов выборок n статистика Х²_n имеет при гипотезе Н₀ простое предельное распределение, не зависящее от гипотезы (т.е. от чисел р⁰_j). Справедливо следующее утверждение.

Теорема 1.1. Если 0 < р⁰_j < 1, j=1, …, N, при n®¥    L(X²_n|H₀)®c²(N-1) [13].

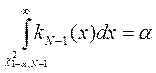На практике предельное распределение c²(N-1) можно использовать с хорошим приближением уже при n³50 и v_j³5. При выполнении этих условий  в соответствии с теоремой 1.1 критическую границу t_a выбирают равной c²_{1-a, N-1}, т. е. (1-a) - квантили распределения  c²(N-1). Действительно, в этом случае Р(Х_n²ÎГ_1a| H₀)=P(Х_n²³c²_{1-a, N-1}| H₀)»

(здесь k_N-1(x) - плотность распределения c²(N-1)).

Таким образом, критерий согласия c² имеет следующий вид: пусть заданы уровень значимости a и объем выборки n и наблюдающиеся значения h=(h₁, … , h_N) вектора частот v=(v₁, … , v_N) удовлетворяют условиям n³50, h_i³5, j=1, …, N; тогда если наблюдавшееся значение t=X_n²(h)статистики (1.11) удовлетворяет неравенству t³ c²_{1-a, N-1}, то гипотезу Н₀ отвергают; в противном случае гипотеза Н₀ не противоречит результатам испытаний.

Сделаем несколько общих замечаний [14]. Критерий согласия c² применяется  в тех случаях, когда в каждом опыте наблюдается одно из N несовместимых событий А₁, … , А_N и заданы частоты появлений этих событий в n испытаниях (говорят также, что наблюдается дискретная случайная величина, принимающая N различных значений). Если же выборка имеет непрерывный закон распределения, то, применяя предварительно метод группировки данных, приходят к рассмотрению дискретной схемы,  которой в качестве событий  А_j рассматриваются события {xÎE_j}, где E₁, ... ,E_N - интервалы группировки. Недостатком метода является то, что группировка данных по классам (интервалам) приводит к некоторой потере информации. Кроме того, остается еще вопрос о выборе числа интервалов N и длине самих интервалов E_j. Однако критерий c² имеет и некоторые достоинства: при его применении нет необходимости учитывать точные значения наблюдений (бывают случаи, когда исходные статистические данные носят не числовой характер). Несомненным преимуществом этого критерия является его универсальность.