Синтез линейных следящих систем. Определение добротности следящей системы по заданной точности

5. Синтез линейных следящих систем

5.1. Методы демпфирования (коррекции) следящих систем.

При проектировании следящих систем различают два основных метода демпфирования.

            Первый метод демпфирования характеризуется отсутствием больших постоянных времени в канале между входом зажимами исполнительного двигателя, что обеспечивает достаточно быстрое нарастание вращающего момента при реверсе двигателя. На рис. 5.1. представлены возможные варианты формирования структурных схем СС, демпфированных по первому методу.

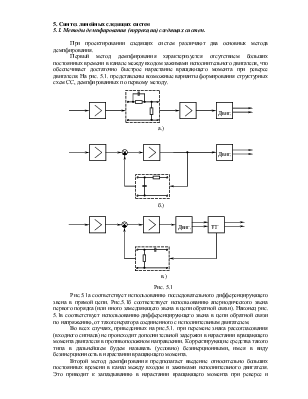
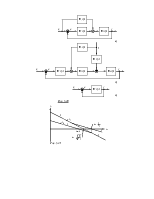
Рис.5.1а соответствует использованию последовательного дифференцирующего звена в прямой цепи. Рис.5.1б соответствует использованию апериодического звена первого порядка (или иного замедляющего звена в цепи обратной связи). Наконец рис. 5.1в соответствует использованию дифференцирующего звена в цепи обратной связи по напряжению, от тахогенератора соединенного с исполнительным двигателем.

Во всех случаях, приведенных на рис.5.1. при перемене знака рассогласования (входного сигнала) не происходит дополнительной задержки в нарастании вращающего момента двигателя в противоположном направлении. Корректирующие средства такого типа в дальнейшем будем называть (условно) безинерционными, имея в виду безинерционность в нарастании вращающего момента.

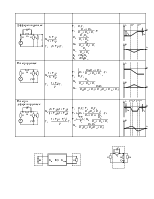
Второй метод демпфирования предполагает введение относительно больших постоянных времени в канал между входом и зажимами исполнительного двигателя. Это приводит к запаздыванию в нарастании вращающего момента при реверсе и появлению, в связи с этим, дополнительных ошибок. На рис.5.2. приведены примеры корректирующих устройств, общим свойством которых является введение дополнительной инерционности в канале управления до зажимов двигателя. Рис.5.2а соответствует использованию в прямой цепи пассивного интегрирующего звена (или интегродифференцирующего). Рис.5.2б соответствует использованию в цепи обратной связи, не охватывающей электродвигатель, дифференцирующего звена. 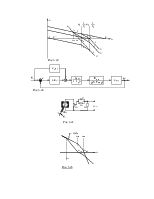Для этих схем характерно введение задержки, что вносит существенные особенности при работе следующей системы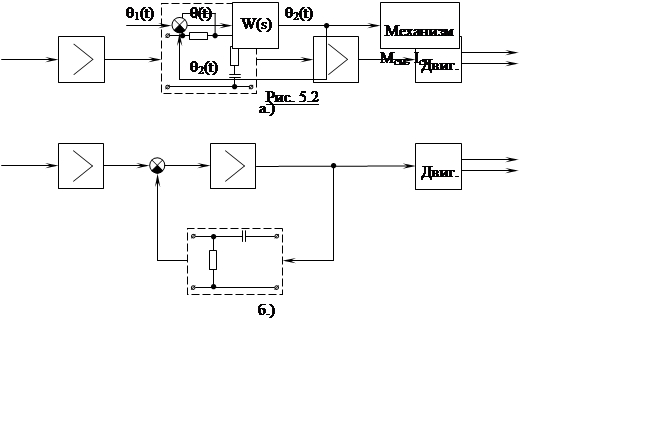
с нелинейным моментом нагрузки от сил трения (сухого).

Корректирующие средства такого типа в дальнейшем будем называть инерционными, имея в виду инерционность в нарастании вращающего момента.

Как будет ясно ниже, два рассмотренных метода демпфирования приводят к различным свойствам следящих систем в отношении плавности их работы на малых скоростях.

5.2. Определение добротности следящей системы (СС) по заданной точности.

5.2.1. Эквивалентный режим работы СС и ошибки.

После выбора исполнительного механизма СС и оптимального его согласования с нагрузкой необходимо перейти к главной проблеме проектирования – обеспечению требуемой точности СС.

Требуемая точность служит определяющим фактором как при расчете системы, так и ее отдельных элементов.

Так как реальный закон изменения входного воздействия заранее не известен, то для определенности задачи проектирования принято испытывать систему некоторым эквивалентным гармоническим сигналом, параметры которого определяются исходя из заданных требований технического задания.

Использование эквивалентного гармонического режима работы СС позволяет с одной стороны вскрыть динамические свойства систем, а с другой – найти сравнительно точные методы оценки ошибок слежения.

Считается, что если следящая система работает с заданной степенью устойчивости и требуемой с точностью при эквивалентном гармоническом воздействии (которой рассматривается как наиболее «тяжелый» режим), то и в реальных условиях точность и устойчивость СС будут в заданных пределах.

Составляющие ошибки СС (рис. 5.2.) при гармоническом воздействии на входе следующие:

-  скоростная ошибка, величина которой пропорциональна или является некоторой функцией скорости вложения;

-  ошибка ускорения, определяемая наличием ускорений при работе СС;

-  моментная ошибка, определяемая наличием момента нагрузки на оси отработки.

Необходимо учитывать также статистическую ошибку системы, связанную с ошибками чувствительных элементов, кинематических передач, дрейфом нуля, усилителя.

qg(t)=q_W+q_e+q_m                                                                                                                                                      (5.1.)

Из задания на проектирование СС имеем:

W_мах     - максимальная скорость отработки;

e _мах         - максимальное ускорение;

q _g        - допустимая динамическая ошибка слежения;

q _cт       - допустимая статистическая ошибка слежения.

На вход системы действует некоторый эквивалентный гармонический сигнал: g(t)=q₁(t)=q_мах sin W_kt                                                                       (5.2.)

Определяя параметры этого режима, получим:

q_1мах=W₁²_мах/ e_1мах;    W_k=e_1мах/W_1мах                                                                        (5.3.)

где:

W_1мах= q_1мW_k;      e_1мах=q_1махW_k²                                                                                                              (5.4.)

Координата контрольной точки при W=W_k

W²1мах__