Синтез линейных следящих систем. Определение добротности следящей системы по заданной точности, страница 2

А_к= 20lg  q_мах e_1мах        = 20 lg q_1мах/q_мах=20 lg W_1махW_1мах/q_махe_1мах=         (5.5.)

= 20 lg KW(W1мах/e1мах)

Движение с постоянной скоростью: g(t)=Wt.

Х_уст.= ½G(p)/ (1+W(p))½_p®0 = W/K_W;      K_W=W/ X _уст.

Движение с постоянным ускорением:

G(t)=et²/2;   x_уст.= ½G(p)/ (1+W(p))½_p®0= e/K_e;       K_e= e/x_уст.;

Движение по гармоническому закону:

G(t)=q₁(t)=q_1maxsin w_kt

X_уст.=½(q₁(p)/ (1+w(p)))p½_p®0;    

p=jwq_maxx_max = q_1max/½1+w(jw_k)½@q_1max/½W(jw_k)½= q_1max/ A(w_k);

L(w_k)= 20 lg A(w_k)=20 lg q_1max/x _max= 20 lg W₁²_max/e_1maxq_max

Требования к низкочастотной части ЛАХ.

q₁(t)=q_1max sin w_kt

q_max= ½F_e(jw_k)½q_1max= q_1max/½1+W(jw_k)½»q_1max/½W(jw_k)½

Чтобы входящее воздействие воспроизводилось с ошибкой не больше        

ЛАХ системы должна проходить не ниже контрольной точки Ак с координатами:

L(w_k)= A_k= 20 lg ½W(jw_k)½= 20 lg q_1max/q_max= 20 lg W²_1max/q_maxe_1max           

W_k=e_1max/W_1max;              q_1max=W²_1max/e_{1max                                                           (*)}

1. Амплитуда скорости  W₁=W_1мах

e₁<e_1мах

Из (*), тогда W_k¯, q_1max  Þ A_k влево по прямой с наклоном 20 db/dec.

В  пределе если e₁=0, w_k®0 это соответствует режиму вращения с постоянной скоростью, для которого q_мах= W_1мах/К_W,

Где К_W - предельное значение для задетой ошибки.

2. e₁=e_1мах

W₁=W_1мах

Из (*) тогда w_k, q_1max¯   Þ A_k вправо по прямой с наклоном 40 db/dec.

W₀²=K_e,  K_e= e_1max/q_max/

5.2.2. Определение добротности СС без учета момента нагрузки (Мсм=0).

Работа СС без учета нагрузки является идеальным случаем, однако рассмотрение такого режима позволяет оценить величины скоростной ошибки и ошибки ускорения, а также яснее представить физику процесса слежения. Учет влияния момента нагрузки в дальнейшем позволит определить добавочную моментальную ошибку и необходимое увеличение добротности системы для обеспечения заданной динамической точности.

Найдем максимальное значение ошибки слежения для случая Мсм=0.

q_1max= q_1max/½1+W(jw_k)½                                                                              (5.6.)

где W(jw_k) - значение частотной передаточной функции разомкнутой системы при частоте входного сигнала  w_k.

Так как в реальных СС  ½1+W(jw_k)½>>1, то выражение (5.6.) можно представить в следующем виде:

q_1max= q_1max/½W(jw_k)½                                                                                  (5.7.)

Учитывая, что частота качки w_k обычно значительно меньше второй сопрягающей частоты w₂ (рис.5.3.) частотная передаточная функция желаемой ЛАХ имеет вид:

K_{W______}               w=w_k

W(jw) » jw(1+jT₁w)                                                                                      (5.8.)

где K_W [1/c]    - добротность системы по скорости.

Определим значение передаточной функции по ошибке при частоте качки w_k из выражения (5.8.) и нейдем выражение для максимальной ошибки по формуле (5.7.):

q_max=½(jw_k(1+T₁w_k) q_1max / K_W ½=½j(W_1мах/К_W) - e_1maxT₁/ K_W ½= W_1мах/К_WÖ1+w₂²T₁²

(5.9.)

Где  W_1мах= w_k q_1max  - амплитуда скорости качки;

e_1max =- w_k²q_{1max -}  амплитуда ускорения качки.

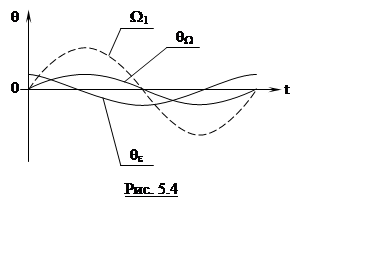
При синусоидальном изменении скорости на входе ошибка, как следует из (5.9.), будет изменяться по закону:

q(t)=q_W+q_e=q_Wmax sin w_kt + q_emaxcos w_kt                                                        (5.10.)

где:

q_W=q_Wmax sin w_kt=W_1мах/К_W sin w_kt                                                   (5.11.)

-  скоростная ошибка, а

q_e=q_emaxcos w_kt= e_1maxT₁/ K_Wcos w_kt=e_max/K_e cos w_kt                                  (5.12.)

-  ошибка ускорения.

Здесь K_e = К_W/ T₁ [1/сек²] - добротность по ускорению.

На рис. 5.4. представлены кривые изменения скорости качки (W₁), скоростной ошибки (q_W) и ошибки ускорения (q_e) .

            Известно, что добротность СС по скорости K_W равна частоте, при которой первая асимптота ЛАХ (рис.5.3.), имеющая наклон – 20 db/dec пересекает ось нуля децибел. Добротность по ускорению K_e равна квадрату частоты, при которой вторая асимптота ЛАХ, имеющая наклон – 40 db/dec пересекает ось нуля децибел, иными словами, K_e равна квадрату базовой частоты w_0.

w0= Ö Ke = Ö КW/ T1