Методическое пособие для подготовки к лабораторным работам по темам: Волновая оптика. Квантовая оптика. Квантовая механика и ядерная физика, страница 9

     j = РBAC + РBCA = (a₁ - b₁) + (a₂ - b₂).

Учтем, что q = b₁ + b₂, тогда

j = (a₁ + a₂) - q.                                                   (4)

Согласно закону преломления sin a₁ /sin b₁ = n и sin a₂ /sin b₂ = n. Откуда

a₁ = arcsin (n sin b₁),

a₂ = arcsin (n sin b₂) = arcsin [n sin(q - b₁)].

Подставляя полученные выражения для a₁ и a₂ в выражение (4), получаем

j = arcsin (n sin b₁) + arcsin [n sin(q - b₁)] - q.                                             (5)

Найдем выражение для минимального угла отклонения, воспользовавшись условием экстремума функции:

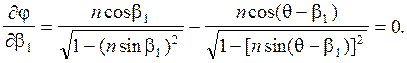                               (6)

Это равенство имеет место при q - b₁ = b₁ и q - b₁ = -b₁. Поскольку q № 0, то физический смысл имеет только условие q - b₁ = b₁. Отсюда вытекает следующее соотношение:

b₁ = q/2.                                                                  (7)

Так как q = b₁ + b₂, то b₁ = b₂. Следовательно, угол отклонения минимален при симметричном расположении падающего на призму и вышедшего из нее лучей. При этом луч внутри призмы параллелен ее основанию. Таким образом, для минимального угла отклонения j_min получаем

j_min = 2 arcsin (n sin q/2) -q.                                  (8)

Отсюда

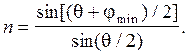                                               (9)

          Измерив углы j_min, можно рассчитать по формуле (9) показатели преломления материала призмы для различных длин волн (при условии, что преломляющий угол призмы известен).

Угловая дисперсия спектральной призмы.

          Призма, как спектральный прибор, характеризуется угловой дисперсией D_j. Угловая дисперсия представляет собой отношение разности углов отклонения dj двух спектрально близких монохроматических пучков к разности их длин волн dl:

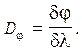                                                       (10)

Угловой дисперсией определяется степень растянутости спектра. Значения  D_j в системе СИ измеряются в радианах на метр (рад/м). Пользуются также внесистемной единицей измерения угловой дисперсии: угловая минута на нанометр (мин/нм).

          Угловую дисперсию можно непосредственно определить по формуле (10), если известны углы отклонения спектрально близких длин волн.

Согласно формуле (9), лучам различной длины волны должны соответствовать разные значения j_min, так как n = ¦(l). Примем во внимание зависимость j от n, а также зависимость n от l. Правую часть уравнения (10) умножим и разделим на dn, тогда для j = j_min

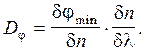                                                  (11)

Продифференцировав формулу (9), получим

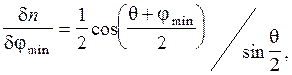                              (12)

тогда (11) преобразуется как

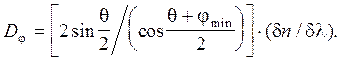                      (13)

Поскольку, как следует из формулы (9),

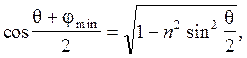                                      (14)

то окончательное выражение для угловой дисперсии призмы принимает вид:

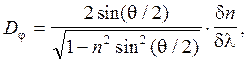                                      (15)

где dn/dl - дисперсия показателя преломления призмы. В том случае, когда преломляющий угол призмы q =60°, формула (15) упрощается:

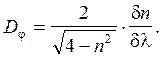                                          (16)

Из формул (15, 16) следует, что угловая дисперсия растет с увеличением n и с увеличением дисперсии материала призмы dn/dl. Поскольку с уменьшением длины волны показатель преломления увеличивается, а также увеличивается дисперсия материала призмы (случай нормальной дисперсии), то и угловая дисперсия в области более коротких длин волн должна быть больше.

Описание установки

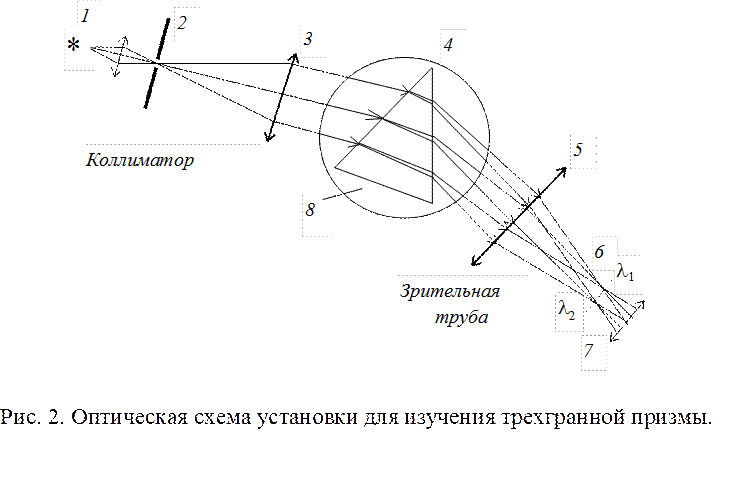
          Оптическая схема установки представлена на рис. 2. Свет от источника 1 падает на щель 2 коллиматора, которая расположена в фокальной плоскости объектива 3 коллиматора. Из объектива коллимированный пучок направляется на призму 4. Если свет немонохроматический, то после преломления в призме произойдет разложение света в спектр. Из призмы выйдут параллельные пучки лучей, соответствующие волнам различной длины l₁, l₂, K . Эти пучки соберутся в фокальной плоскости 6 объектива 5 зрительной трубы в виде спектра, являющегося изображением щели 2. Спектр наблюдается глазом через окуляр 7. Коллиматор и зрительная труба смонтированы на массивном основании. Коллиматор укреплен неподвижно, а зрительная труба может вращаться в горизонтальной плоскости. Исследуемая призма устанавливается на предметный столик гониометра 8. Через нижний окуляр зрительной трубы наблюдается отсчетная шкала, с помощью которой определяют угол, образованный оптическими осями коллиматора и зрительной трубы. Описание гониометра см. в работе  «Определение длин волн с помощью отражательной дифракционной решетки».

Порядок выполнения работы

1. Включить через блок питания газоразрядную ртутную лампу и осветить щель коллиматора. Повернуть зрительную трубу таким образом, чтобы оптические оси зрительной трубы и коллиматора образовывали единую прямую, а в поле зрения окуляра было видно изображение щели коллиматора. Сфокусировать зрительную трубу на это изображение, установить перекрестье окуляра на середину изображения щели. В этом положении измерить угол a₀ (поправка на нуль).

2. Поместить на столик гониометра исследуемую призму так, чтобы биссектриса ее преломляющего угла была приблизительно перпендикулярна оси коллиматора. Поворачивая рукой столик с призмой и вращая зрительную трубу, отыскать спектр. Установить зрительную трубу гониометра так, чтобы в окуляр были видны две желтые линии (дублет) спектра ртути. Медленно вращать столик с призмой в направлении уменьшения угла отклонения (к основанию призмы) и следовать зрительной трубой за перемещающейся спектральной линией. Уловить момент, когда изображение щели остановится и начнет двигаться в противоположном направлении при неизменном направлении вращения столика.