Методическое пособие для подготовки к лабораторным работам по темам: Волновая оптика. Квантовая оптика. Квантовая механика и ядерная физика, страница 12

Результаты измерений углов и вычислений длин волн спектральных линий

Порядок спектра, m	Цвет линии	a		j		l, нм
		…°..¢..¢¢	…,….°		…,….°
1	1 2 3 4 5
2	–¢¢–
…	–¢¢–
5	–¢¢–

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ВРАЩЕНИЯ И КОНЦЕНТРАЦИИ

ОПТИЧЕСКИ АКТИВНОГО РАСТВОРА ПРИ ПОМОЩИ ПОЛЯРИМЕТРА

Цель работы: ознакомиться с теорией поляризованного света, принципами устройства поляриметров, методики поляризационных измерений и определить концентрацию сахарного раствора при помощи поляриметров Корну и СМ.

Приборы и принадлежности: поляриметры, кюветы с сахарным раствором.

Теоретическое введение

Свет представляет собой электромагнитные волны. График электромагнитной волны представлен на рис. 1, а ее уравнение имеет вид

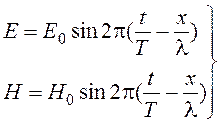                                          (1)

где Е и Н - напряженности электрического и магнитного полей.

Плоскость, проходящая через вектор  и направление распространения волны x , называется плоскостью колебаний.

         Плоскость, проходящая через направление  распространения волны и вектор , называется плоскостью поляризации

Опыт показывают, что в основном все действия света: химическое, биологическое и др. обусловлены электрической составляющей световой волны. Поэтому в дальнейшем будем говорить только о плоскости колебаний вектора , подразумевая, что плоскость поляризации всегда неразрывно с ней связана и всегда перпендикулярна ей.

Свет, в котором колебания вектора совершаются в строго определенном направлении, называется плоскополяризованным светом.

Свет, в котором вектор  имеет всевозможные направления колебаний, причем ни одно из этих направлений не является преимущественным, называется естественным светом.

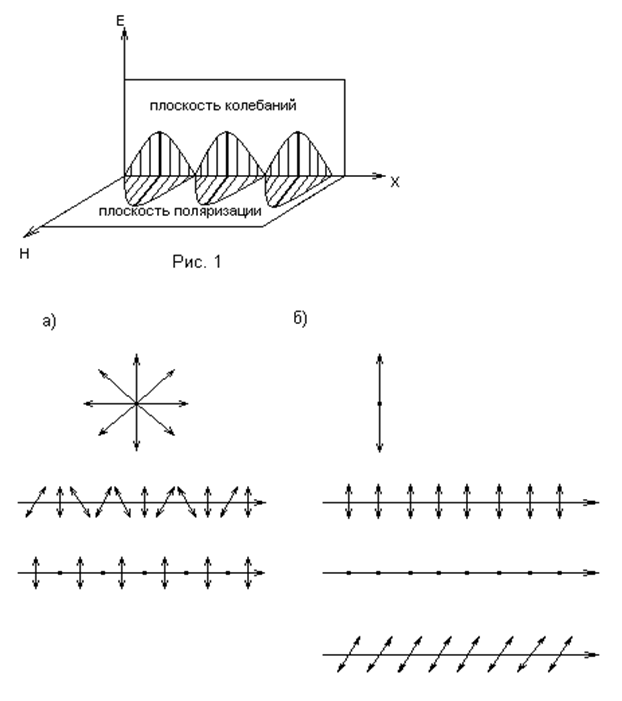
Рис. 2.  График электромагнитной волны: а) условное изображение естественного (неполяризованного) луча; б) условное изображение плоскополяризованного луча.

На рис, 2 схематично показаны направления колебаний вектора для естественного (а) и плоскополяризованного (б) света. При этом верхние рисунки изображают луч, направленный перпендикулярно плоскости рисунка, а стрелки указывают направление колебаний вектора . На нижних рисунках показаны условные обозначения соответствующих лучей.

          Каждый атом излучает плоскополяризованную волну, но так как любой источник представляет совокупность множества атомов, каждый из которых излучает волну с некоторой произвольной ориентацией вектора , то все источники излучают свет естественный.

Для получения плоскополяризованного света служат специальные устройства, называемые поляризаторами. Основное свойство этих устройств заключается в том, что из всей совокупности волн с различно ориентированными плоскостями колебаний они пропускают лишь те, плоскости колебаний которых совпадают с направлением оптической оси поляризатора.

Закон Малюса

Рассмотрим прохождение света через два поляризационных устройства (рис.3). Пройдя через первое поляризационное устройство Р (поляризатор), свет становится плоскополяризованным. Второе поляризационное устройство А (анализатор) может пропустить только те колебания, которые совпадают с направлением его оптической оси. Если оптические оси поляризатора и анализатора совпадают, то интенсивность проходящего света будет максимальной. Если оптические оси составляют между собой угол 90^º, то интенсивность проходящего света будет равна нулю. Такое положение поляризатора и анализатора называется скрещенным. 

В том случае, когда оптические оси поляризатора и анализатора составляют между собой некоторый угол j, интенсивность проходящего света будет принимать промежуточное значение. Найдем зависимость интенсивности света, вышедшего из анализатора, от угла j.

Пусть Е_р(рис. 4) — амплитуда световой волны, прошедшей через поляризатор Р. Амплитуду Е_р можно разложить на две составляющие Е_А и Е_^ первая из которых совпадает с направлением оптической оси анализатора, а вторая перпендикулярна ей. Составляющая световой волны с амплитудой Е_А  пройдет через анализатор, а составляющая с амплитудой Е_^ будет задержана анализатором. 

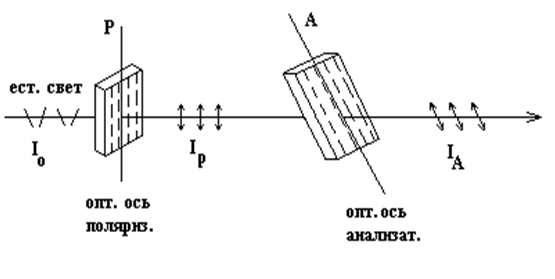Рис. 3. Прохождение света через поляризатор и анализатор.

Из векторной диаграммы на рис. 4 следует, что амплитуда световых колебаний, выходящих из анализатора, равна

                                                                        (2)

Так как интенсивность колебаний пропорциональна квадрату амплитуды (I~E²), то из выражения (2) в квадрат получим

                                                                        (3)

Это выражение носит название закона Малюса, где I_P — интенсивность плоскополяризованного света, вышедшего из поляризатора и падающего на анализатор; I_A — интенсивность света, вышедшего из анализатора; j — угол между оптическими осями поляризатора и анализатора.

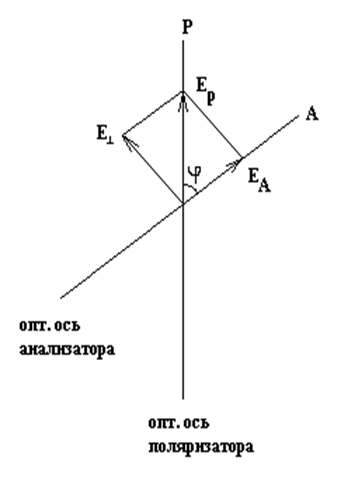
Рис. 4. Векторная диаграмма, поясняющая закон Малюса.

Таким образом, при вращении анализатора вокруг луча освещенность поля зрения будет изменяться от максимума (при j =0) до нуля (при j=90^°).

Вращение плоскости колебаний

Опыт показывает, что при прохождении плоскополяризованного света через некоторые вещества плоскость его колебаний поворачивается на некоторый угол. Вещества, вращающие плоскость колебаний, называются оптически активными. К ним относятся сахар, кварц, винная кислота, скипидар и многие другие кристаллические и аморфные вещества.

Одни вещества вращают плоскость колебаний по часовой стрелке, если смотреть вдоль светового пучка, другие — против часовой стрелки. Первые называются правовращающими, вторые — левовращающие. Например, свекловичный сахар является правовращающим, а фруктовый—левовращающим. Кварц встречается в обеих модификациях.