6. Сравнить случайную и приборную погрешности и определить полную погрешность каждого прямого измерения - ∆u, ∆v, ∆w, … . При этом возможны три случая, рассмотрим их на примере величины u.
Если ∆uпр > ∆uсл в три и более раз, то полагаем, что ∆u ≈ ∆uпр
Если ∆uсл >∆uпр в три и более раз, то полагаем, что ∆u ≈ ∆uсл
В этом случае погрешность ∆uсл можно уменьшить, увеличивая число измерений n .
Если случайная погрешность и приборная погрешность сравнимы по величине ∆uсл ≈ ∆uпр, то следует их сложить по правилу
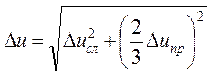 (6.6)
(6.6)
7. Рассчитать погрешность косвенного измерения ∆f по формуле (5.5). Если рабочая формула (6.1) имеет степенной вид, то для расчета ∆f использовать формулу (5.7).
6. Окончательный результат измерения записать в следующем виде:
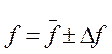 (6.7)
(6.7)
с указанием величины относительной погрешности (необязательное требование):
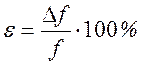 (6.8)
(6.8)
В результате измерений прямых или косвенных, как уже отмечалось, получаются приближённые числа. Цифры, составляющие приближённое число, могут быть верными, сомнительными и неверными. Цифра называется верной, если абсолютная погрешность числа меньше одной единицы разряда этой цифры. Цифры, стоящие слева от верной, также будут верными. Цифра называется сомнительной, если её разряд совпадает с разрядом первой значащей цифры погрешности. Все цифры, стоящие справа от сомнительной, будут неверными. Так, в числе 381,6±1 цифры 3 и 8 - верные, 1 - сомнительная, 6 - неверная.
При проведении вычислений в лабораторных работах исходными данными служат результаты прямых измерений, последняя цифра в них обычно является сомнительной. Кроме того, в вычислениях используются табличные данные и различные физические постоянные. Следует отметить, что мировые постоянные, взятые из таблиц, содержат только верные цифры, а за погрешность табличных данных, если она не указана, принимают ±0,5 разряда последней значащей цифры.
Отметим, что при проведении косвенных измерений в расчетах выполняются математические операции над приближенными числами, определяемыми с различной точностью. При этом руководствуются следующими правилами округлений и вычислений.
1.При сложении и вычитании приближенных чисел в
результате сохраняют столько разрядов (цифр после запятой), сколько их
содержится в числе с наименьшим количеством разрядов.
2. При умножении и делении в результате сохраняют столько значащих цифр,
сколько их содержится в числе с наименьшим количеством значащих цифр.
3. Результат расчета значений функций
![]() некоторого приближенного числа
x должен содержать столько значащих цифр, сколько их имеется в числе x.
некоторого приближенного числа
x должен содержать столько значащих цифр, сколько их имеется в числе x.
4. В промежуточных расчетах допускается использовать на одну - две значащие цифры больше (“с запасом”).
Основное требование, предъявляемое к расчёту, заключается в том, чтобы проводимые вычисления не вносили в результат дополнительной погрешности. При использовании вычислительной техники это требование обычно выполняется, однако окончательный результат и его абсолютная погрешность могут содержать много цифр, количество которых определяется, например, разрядностью табло используемого калькулятора. Необходимо помнить, что запись приближённых чисел сизлишне большим количеством знаков создаёт лишь иллюзию высокой точности.
При окончательной записи результата необходимо руководствоваться следующими правилами:
1. Абсолютную погрешность следует округлить до одной значащей цифры.
2. Результат округлить так, чтобы его последняя цифра находилась в том же разряде, что и единственная значащая цифра погрешности.
3. Общий десятичный множитель результата и погрешности вынести за скобки.
Приведём несколько примеров окончательной записи результатов.
Неправильно Правильно
(534,031 ± 0,043) м (534,03 ± 0,04) м
(14,275 ± 1,17) В (14 ± 1) В
(1587 ± 281,6) с (16 ± 3)∙102 с
(1,965∙10-19 ± 3,81∙10-21) Кл (1,96 ± 0.04) 10-19 Кл
В физике и технике результаты измерений очень часто изображают в виде графических зависимостей. Графики дают наглядное представление о полученных результатах, позволяют графически определить некоторые величины, сравнить эксперимент и теорию. В настоящее время существует достаточно большое число программ со встроенными графическими редакторами, среди которых наиболее популярны Origin и Excel. Оформление работ на компьютере приветствуется. Тем не менее, студенты должны владеть навыками построения графиков вручную. Для этого рассмотрим основные правила построения графиков, многим из которых необходимо следовать и при построения графиков с помощью компьютера.
1. Графики следует строить на миллиметровой бумаге; лучше это делать карандашом. Каждый график должен иметь заголовок. Оси координат проводят по линейке и на них через равные промежутки (если масштаб не логарифмический) наносят масштабные метки. (Равноотстоящие друг от друга деления масштаба обеспечивают как удобство работы с графиком, так и удобство его зрительного восприятия.) Расстояние между метками по оси абсцисс и ординат можно выбирать различным.
2. Масштабы и начала отсчета по координатным осям выбираются так, чтобы изображение зависимости занимало большую часть поля чертежа и чтобы из графика можно было получить максимум полезной информации. Так, на рис. 8.1 (б) масштаб выбран верно в отличие от рис. 8.1 (а). Для линейных зависимостей масштаб по осям выбирается таким, чтобы угол наклона линии соответствовал бы приблизительно 45°. Заметим, что на пересечении осей не обязательно должны находиться нулевые значения величин. При выборе масштаба необходимо помнить, что точность построения графика должна быть не ниже точности измерений. Это требование особенно актуально для тех случаев, когда из графика определяются те или иные физические величины, например, при обработке линейных зависимостей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.