4. По
формуле 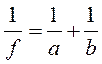 для каждого опыта вычислить фокусное расстояние собирающей
линзы.
для каждого опыта вычислить фокусное расстояние собирающей
линзы.
5. Вычислить приближенное значение f, абсолютную и относительную погрешности методом Стьюдента. Окончательный результат записать в виде f=fпр±Df
6.
Вычислить оптическую силу линзы 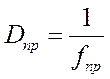
Таблица 1
Результаты измерений для собирающей линзы.
|
№ п/п |
a |
b |
f |
fпр |
Df |
|
1 2 3 4 5 |
II часть.Определение фокусного расстояния рассеивающей линзы.
1. Расположить на оптической скамье предмет, собирающую линзу и экран.
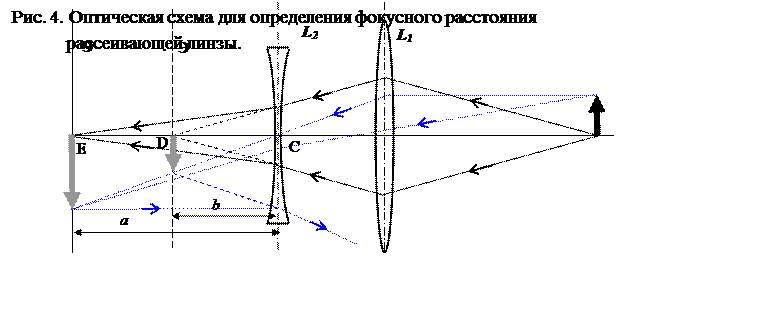
2. Измерить по шкале положение экрана, соответствующее резкому изображению предмета. Обозначить его точкой D (см. рис. 4).
3. Между собирающей линзой L1 и точкой D поместить рассеивающую линзу L2. Перемещением экрана добиться резкого изображения предмета; это положение обозначено точкой Е. Если принять, что для линзы L1 предметом является изображение в плоскости, проходящей через точку Е, то EC=a и DC=b.
4. 
Повторить измерения пять раз
для разных положений линзы и экрана и полученные результаты занести в таблицу,
аналогичную предыдущей.
5. По формуле (2) с учетом знаков b и f вычислить фокусное расстояние рассеивающей линзы L2 для каждого опыта.
6. Из полученных значений f вычислить приближенное значение, абсолютную и относительную ошибки. Окончательный результат записать в виде: f=fпр±Df
7. Вычислить оптическую силу линзы 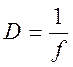 .
.
1. Что такое линза? Какую линзу называют тонкой, собирающей, рассеивающей?
2. Запишите формулу тонкой линзы.
3. Дайте определение фокуса, фокусного расстояния, оптической силы линзы.
4. Постройте изображение предмета в собирающей линзе при условиях f<a<2f, a=2f, a>2f, a<f .
5. Может ли собирающая линза рассеивать лучи? Ответ аргументируйте с помощью оптической схемы.
6. Что такое линейное увеличение линзы? От чего оно зависит?
7. Пояснить сущность методов определения фокусного расстояния собирающей и рассеивающей линз.
8. Построить изображение предмета в рассеивающей линзе. Построить в рассеивающей линзе изображение точки, находящейся на главной оптической оси линзы.
9. Вывести формулу для вычисления фокусного расстояния рассеивающей линзы в соответствии с проделанным экспериментом.
ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ РАСТВОРА ПРИ ПОМОЩИ
ФОТОМЕТРА ПУЛЬФРИХА И ФОТОЭЛЕКТРОКОЛОРИМЕТРА
ФЭК-56
Цель работы – построить кривую поглощения окрашенного раствора и определить его концентрацию.
Приборы и принадлежности: фотометра Пульфриха (или ФЭК-56), кюветы, растворы с различной концентрацией, дистиллированная вода.
Теоретическое введение
Измерение концентрации окрашенного раствора с помощью фотометра Пульфриха или фотоэлектроколориметра основано на явлении поглощения видимого света.
Поглощение – это превращение световой энергии во внутреннюю энергию вещества, через которое проходит световая волна. Вследствие поглощения энергия светового пучка уменьшается. Если среда неоднородная (мутная), то энергия светового пучка, по мере его прохождения через среду, уменьшается за счет рассеяния. Наличие окраски – признак поглощения света в видимой области. Действительно, если бы все видимые лучи белого света прошли бы без поглощения, то на выходе из раствора они создали бы ощущение того же белого света, и раствор был бы бесцветным.
Поглощение света можно описать следующим образом. Пусть на поверхность прозрачной однородной среды толщиной xнормально к поверхности падает параллельный пучок световых лучей с интенсивностью I0. Выделим в данной среде бесконечно тонкий слой толщиной dx (рис.1).
Количество световой энергии dI, поглощенное этим слоем, можно принять пропорциональным его толщине и интенсивности падающего на него света
![]() (1)
(1)
Знак минус указывает на то, что интенсивность света убывает на отрезке dx.
Коэффициент пропорциональности k называется коэффициентом поглощения. Коэффициент поглощения выражает относительное поглощение света на единице длины поглощающего вещества. Он определяется свойствами поглощающей среды и при прочих равных условиях зависит от длины волны. При умеренных плотностях облучения ни от интенсивности падающего света, ни от толщины слоя коэффициент поглощения не зависит.
Чтобы получить связь между интенсивностью и толщиной слоя при конечных значениях толщины x, нужно проинтегрировать выражение (1).
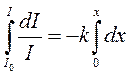 ;
;
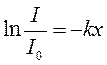 .
.
После потенцирования получим
![]() ,
(2)
,
(2)
где I0 – интенсивность света, падающего на поглощающий слой,
I – интенсивность света, вышедшего из слоя толщиной x.
Формула (2) называется законом Бугера.
Поглощение света носит селективный характер, т.е. на различных длинах волн наблюдается разное поглощение. Этим объясняется окрашенность поглощающих сред. Например, стекло, слабо поглощающее красные и оранжевые лучи и сильно поглощающее зеленые, синие и фиолетовые при осмотре в белом свете будет окрашенным в красный цвет. Если же на такое стекло направить зеленый, синий или фиолетовый свет, то из-за сильного поглощения света данной длины волны стекло покажется «черным».
Среда, которая не поглощает ни на какой длине волны в в видимой области, будет абсолютно прозрачной.
Зависимость коэффициента поглощения от длины волны не выражается универсальной формулой. Эта зависимость обычно изображается кривой с одним или несколькими максимумами (см. рис.2). График зависимости k=k(l) называется кривой поглощения.
В случае растворов коэффициент поглощения зависит также от концентрации растворенного вещества. Бером было найдено, что при малых концентрациях коэффициент поглощения k пропорционален концентрации раствора
k=ec, (3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.