Методическое пособие для подготовки к лабораторным работам по темам: Волновая оптика. Квантовая оптика. Квантовая механика и ядерная физика, страница 16

      Число m зон Френеля при заданной ширине щели a и длине волны l зависит от угла дифракции j:

m = 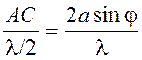.                                               (2)

Для всех углов дифракции, при которых в щели уложится четное число зон Френеля (m = 2k), будут наблюдаться дифракционные минимумы (темные полосы), т.к. зоны попарно погасят друг друга:

asinj = ± 2k;                                                      (3)

для всех углов дифракции, при которых в щели уложится нечетное число зон Френеля (m = 2k + 1), будут наблюдаться дифракционные максимумы, т.к. одна зона останется непогашенной:

asinj = ± (2k + 1).                                             (4)

Величина k = 1, 2, 3 … называется порядком дифракционного максимума (минимума).

       Ширина дифракционного максимума (расстояние между двумя ограничивающими его дифракционными минимумами) зависит от ширины щели a, длины световой волны l и от расстояния между щелью и экраном l. Если щель очень узкая (a < l), то вся поверхность AB будет представлять собой лишь часть одной зоны, и условие даже первого минимума не может быть выполнено ни при каком угле дифракции. Весь экран будет освещен, причем освещенность будет убывать от центра экрана к его краю.  Если щель широкая (a >> l), то на экране возникнет изображение щели, окаймленное по краям очень узкими практически неразличимыми глазом чередующимися темными и светлыми полосами. Если же размер щели соответствует условию (1), то будет наблюдаться отчетливая дифракционная картина, распределение интенсивности I света в которой имеет вид, показанный на рис. 5.

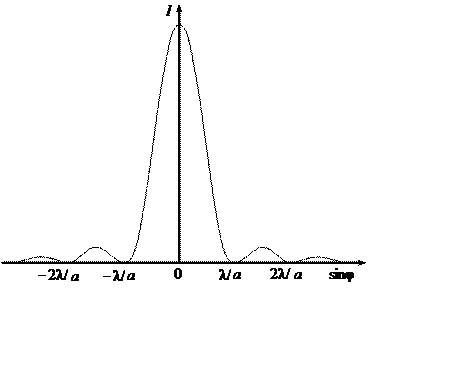Рис. 5. Распределение интенсивности в дифракционной картине при дифракции на узкой щели.

        Соотношение интенсивностей в дифракционной картине можно определить по методу графического сложения амплитуд (рис.6). Разобьем фронт волны на элементарные зоны, ширина которых значительно меньше, чем ширина зон Френеля. Каждая такая элементарная зона будет играть роль вторичного источника света. Пусть DA – амплитуда колебаний волны от одной элементарной зоны; d – разность фаз волн от двух соседних элементарных зон (d зависит от угла дифракции j). Амплитуда A результирующего колебания в данной точке экрана представляет собой геометрическую сумму векторов элементарных амплитуд .

Рассмотрим результаты сложения амплитуд.

    Рис.6. Иллюстрация метода графического сложения амплитуд.

1. Пусть угол дифракции j равен 0. В этом случае разность фаз колебаний d равна нулю. Элементарные векторы  имеют одинаковое направление (рис. 6 а), и амплитуда результирующего колебания A₀ равна алгебраической сумме амплитуд DA. Получаем максимальное значение результирующей амплитуды, соответствующее центральному дифракционному максимуму.

      2. Пусть при некотором угле дифракции j разность фаз колебаний, соответствующих краям щели, d равна p. В этом случае все векторы  должны располагаться вдоль полуокружности длиной A₀ (рис. 6 б), тогда векторы  от элементарных зон у краев щели будут иметь противоположное направление. Результирующая амплитуда A является диаметром полуокружности. Т.к. длина полуокружности A₀ = , то результирующая амплитуда A = .

      3. Пусть разность фаз колебаний, соответствующих краям щели, равна 2p. Векторы  расположатся вдоль окружности длиной A₀ (рис. 6 в). Результирующая амплитуда равна нулю, что соответствует дифракционному минимуму первого порядка.

      4. Пусть разность фаз колебаний от краев щели равна 3p. Векторы  обойдут полтора раза окружность диаметра A₁ (рис. 6 г). Возникает дифракционный максимум первого порядка. Величину амплитуды можно найти из условия pA₁ +  = A₀ (длина окружности плюс длина полуокружности). Отсюда A₁ = .

      Аналогично можно определить амплитуды колебаний, соответствующих последующим максимумам:

A₂ = , A₃ = , …  A_n = .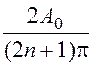

      Поскольку интенсивность света I пропорциональна квадрату амплитуды, соотношение интенсивностей света в дифракционной картине можно представить как отношение квадратов соответствующих амплитуд:

I₀ : I₁ : I₂ : I₃ : … I_n =  :  :  :  : … .                              (5)

Принимая интенсивность света центрального максимума за единицу, получим:

I₀ : I₁ : I₂ : I₃ :… I_n = 1 : 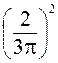: : 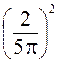: 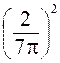… 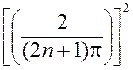,                (6)

или

I₀ : I₁ : I₂ : I₃… : I_n = 1 : 0,045 : 0,016 : 0,008 : …

Таким образом, центральный максимум значительно превосходит по интенсивности остальные максимумы. В нем сосредоточена основная доля (» 90%) светового потока, проходящего через щель.

Описание установки

      В качестве источника света в работе используется лазер, излучение которого характеризуется рядом особенностей: высокой степенью когерентности, высокой интенсивностью и малой угловой расходимостью. Световые пучок, излучаемый лазером, состоит из практически параллельных лучей и не требуют применения оптических систем для их коллимации.

      Если на пути лазерного луча поставить щель, то на экране будет наблюдаться дифракционная картина (рис. 5). Схема установки приведена на рис. 7. На оптической скамье 1 установлены гелий-неоновый лазер 2, рейтеры 3 для крепления дифракционных щелей 4 (дифрешеток, рамок с нитями и др. объектов), съемный экран 5.

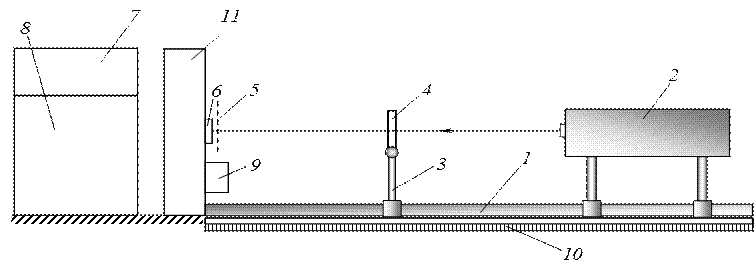      Рис.7. Схема установки для наблюдения дифракции от узкой щели.

      Для исследования распределения интенсивности света в дифракционной картине используется фотодиод 6. Возникающая под воздействием света фотоэдс усиливается с помощью гальванометрического усилителя 7. Регистрация сигнала осуществляется автоматическим потенциометром (самописцем) 8 на диаграммной ленте. Фотодиод укреплен на каретке и с помощью электродвигателя 9 может перемещаться с небольшой скоростью по обе стороны от среднего положения. Для отсчета положения рейтеров относительно экрана оптическая скамья снабжена линейкой 10. Механизм перемещения фотодиода помещен внутри блока 11.