1. Ознакомиться с устройством и принципом действия гелий-неонового лазера (см. описание к работе «Определение длины волны излучения оптического квантового генератора»).
2. Установить на оптической скамье рейтер с узкой щелью. Закрепить съемный экран.
3. Включить лазер.
4. Перемещениями установить щель так, чтобы лазерный луч попадал по центру щели перпендикулярно ее плоскости. Регулировкой ширины щели получить на экране четкую дифракционную картину.
5. Измерить расстояния xk между минимумами интенсивности на экране. Измерить расстояние l от щели до экрана. Результаты измерений занести в таблицу.
Таблица результатов эксперимента по дифракции на узкой щели.
|
k |
xk, мм |
l, см |
a, мкм |
|
1 |
|||
|
2 |
|||
|
… |
|||
|
5 |
6. Из условия дифракционных минимумов
(3) с учетом соотношения sinj » tgj = ![]() , справедливого для малых углов дифракции, вычислить ширину дифракционной
щели по формуле
, справедливого для малых углов дифракции, вычислить ширину дифракционной
щели по формуле
a = 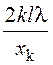 ,
,
где k – порядок дифракционного минимума, l – расстояние от щели до экрана, xk – расстояние между дифракционными минимумами порядка k. Результаты вычислений занести в таблицу.
7. Вычислить приближенное (среднее арифметическое) значение ширины щели aср, абсолютную Da и относительную Da/aср погрешности. Результат записать в виде a = (aср ± Da) мкм.
8. Снять экран. Установить фотодиод в среднее положение (включение механизма перемещения осуществляется тумблерами на передней панели блока).
9. Включить гальванометрический усилитель и автоматический потенциометр (самописец). Получить на диаграммной ленте кривые распределения интенсивности света в дифракционной картине. Полученные кривые приложить к отчету.
10. Рассчитать соотношение интенсивностей I0 : I1 : I2 : I3 и сравнить его с теоретическим.
11. Написать выводы по работе.
1. В чем заключается явление дифракции? Каковы оптимальные условия для наблюдения дифракции?
2. Как формулируется принцип Гюйгенса – Френеля?
3. Чем отличается дифракция Фраунгофера от дифракции Френеля? Приведите схемы получения сферических и плоских волн.
4. Обоснуйте условия образования максимумов и минимумов при дифракции от щели.
5. Как будет меняться дифракционная картина при сужении (расширении) щели? При уменьшении (увеличении) длины волны?
6. Как с помощью метода графического сложения амплитуд получить соотношение между интенсивностями света в дифракционной картине?
Часть IX. Квантовая оптика
ОПРЕДЕЛЕНИЯ ПОСТОЯННОЙ СТЕФАНА-БОЛЬЦМАНА
С ПОМОЩЬЮ ОПТИЧЕСКОГО ПИРОМЕТРА
Цель работы: определить постоянную Стефана-Больцмана посредством изучения излучения нечерного тела - вольфрамовой спирали.
Приборы и принадлежности: оптический пирометр с исчезающей нитью, лампа накаливания с вольфрамовой спиралью, трансформатор, амперметр, вольтметр, источник постоянного тока Б5-30.
Теоретическое введение
Электромагнитное излучение, причиной которого является возбуждение атомов и молекул вещества вследствие их теплового движения, называется тепловым излучением. Наиболее просто законы теплового излучения формулируются для так называемого абсолютно черного тела. Под последним понимают тело, целиком поглощающее всю падающую на него лучистую энергию. По поглощающим свойствам к абсолютно черному телу близки такие вещества, как: сажа, платиновая чернь, черный бархат. Хорошей моделью абсолютно черного тела является полость с малым отверстием.
Важной характеристикой теплового излучения является интегральная испускательная способность (интегральная светимость) RT излучающей поверхности. Она представляет собой энергию, излучаемую с единицы площади за единицу времени во всем интервале длин волн
RT = (1)
Здесь Wизл - количество излученной энергии с поверхности S за время t.
Стефан и Больцман установили, что интегральная испускательная способность абсолютно черного тела RАЧТ пропорциональна четвертой степени абсолютной температуры, т.е.
RАЧТ= s T4 (2)
Коэффициент
пропорциональности s, получивший название постоянной Стефана-Болъцмана, является универсальной
постоянной.
Для нечерных тел на основании закона Кирхгофа вместо (2) можно записать
RT = a s T4
или
RT = a RАЧТ (3)
где a - интегральная поглощательная способность тела. Она
показывает, какая доля равновесного излучения, падающего на тело, поглощается
этим телом
a = (4)
Поглощательная способность тела зависит от температуры и различна для разных тел. Для абсолютно черного тела a = 1.
Если тело находится в тепловом равновесии с окружающей средой, то количество энергии, излучаемой телом, должно быть равно количеству поглощаемой энергии Wизл = Wпогл. Поскольку Wизл = R S t, а Wпогл = a Wпад, то R S t = a Wпад. С учетом уравнения (3) имеем
Wпад = RАЧТ S t (5)
На основании этого можно сделать вывод: при тепловом равновесии на поверхность любого тела падает столько энергии, сколько излучалось бы этим телом, если бы его поверхность была абсолютно черной.
Рассмотрим неравновесное стационарное излучение вольфрамовой спирали, когда ее температура Т отличается от температуры окружающей среды Т0 (Т > Т0),
Спираль нагревается электрическим током и потребляет мощность N = U I, где U и I – соответственно, напряжение и сила тока. Кроме того, спираль поглощает часть падающего на нее излучения, которое зависит от температуры окружающих тел и будет таким же, как при тепловом равновесии при температуре Т0.
В соответствии с формулой (5) за 1 сек на спираль падает энергия
RАЧТ S = s T04 S
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.