Методическое пособие для подготовки к лабораторным работам по темам: Волновая оптика. Квантовая оптика. Квантовая механика и ядерная физика, страница 25

Обозначив буквами X и Y химические символы элементов превращения, происходящие при радиоактивном распаде нуклидов, можно отобразить следующими ядерными реакциями:

-  α-распад:

          _zX^A → _z-2Y^A-4 + ₂He⁴ ;

- β-распад:

_zX^A → _z+1Y^A + _-1e⁰ + ΰ,

- γ -распад:

_zX*^A → _zX^A + hν.

          Испускаемые частицы обладают разной проникающей способностью. Например, в воздухе α-частицы проходят путь в несколько сантиметров, но полностью задерживаются тонким листом бумаги. Проникающая способность β-частиц гораздо выше. В воздухе они способны пройти путь в несколько метров, а в твердых телах до нескольких миллиметров. Наивысшей проникающей способностью обладает γ-излучение. Оно свободно преодолевает слои стали, силикатных строительных материалов и т.п. в несколько сантиметров и более.

          Проходя через вещество, радиоактивные частицы взаимодействуют с ним, образуя вдоль своего пути множество пар ионов. Так α-частица способна создать около 10⁵ пар ионов.  Ионизирующая способность β-частиц сильно зависит от их энергии и в среднем на 2-3 порядка ниже, чем у α-частиц, а эффективность ионизации вещества  γ-излучением еще ниже.

          Воздействие радиоактивного излучения на вещество пропорционально числу элементарных частиц или ядерных фрагментов, образующихся при распаде. В качестве характеристики последнего процесса используют понятие «активность радиоактивного источника». Под активностью некоторого количества радиоактивного препарата понимают число распадов, происходящих в нем за единицу времени. В системе единиц СИ за единицу активности принимается беккерель (Бк), соответствующий 1 расп/с. В качестве внесистемной единицы часто используется кюри (Ки). Единица активности Ки соответствует 3,7∙10¹⁰ расп/с (такое число распадов происходит за 1 с в 1 г радия).

          Активность препарата пропорциональна числу нераспавшихся ядер и уменьшается во времени по экспоненциальному закону

N=N₀∙e^-λt ,                                                                     (1)

где N₀ – число ядер в начальный момент времени,

N –число ядер, не распавшихся к моменту времени t,

λ – постоянная распада, характерная для данного радиоактивного препарата.

          Часто при описании радиоактивного препарата используется понятие периода полураспада Т_1/2. Это время, за которое распадается половина первоначального количества радиоактивных ядер.

Положив в уравнении (1) N=N₀/2 и обозначив t=T_1/2, получим

T_1/2= ln2/ λ .                                                                                    (2)

Для нуклидов различных элементов период полураспада лежит в диапазоне от долей секунды до миллиардов лет. Некоторые нуклиды настолько стабильны, что их самопроизвольный распад наблюдать не удается.   

При прохождении β-частиц через какой-либо материал наблюдается их поглощение. По мере проникновения в материал число β-частиц уменьшается примерно по экспоненциальному закону. Типичная кривая, получаемая при измерении числа прошедших через материал β-частиц в зависимости от толщины поглощающего слоя, показана на Рис.1. Заметим, что в измерения вносит вклад естественный радиационный фон, представляющий собой космическое излучение, а также γ-излучение природного нуклида ₁₉К⁴⁰ и нуклидов  уранового и ториевого рядов, всегда присутствующих в элементах конструкции зданий, в предметах, наполняющих помещения, и даже в телах работающих в помещениях людей. Чем больше энергия β-частиц, тем глубже они проникают в материал.

Как следует из Рис. 1, кривая поглощения, отражающая зависимость числа β-частиц N, прошедших через материал от толщины поглощающего слоя δ, асимптотически приближается к фону N_ф. Это позволяет определить максимальную глубину δ_макс проникновения β-частиц в материал. Если представить зависимость N(δ) в координатах [ln(N– N_ф), δ], то она окажется приблизительно линейной, и величина δ_макс будет равна отрезку, отсекаемому этой прямой на оси абсцисс (Рис.2).

Для β-частиц с энергией выше 0,6 МэВ между глубиной их проникновения  δ и энергией существуют эмпирическое соотношение 

ρ∙δ_макс = АЕ_макс – В,                                                            (3)

где А и В – некоторые эмпирические постоянные, а ρ – плотность поглощающего материала.

Для алюминия соотношение (3) может быть представлено как

Е_макс = 5∙δ_макс + 0,245  (МэВ),                                    (4)

Таким образом, определив из опыта максимальную глубину проникновения β-частиц в алюминий, можно по формуле (4) рассчитать их максимальную энергию.

Экспериментальная часть

Для проведения опыта используется радиометр Б-4, состоящий из коробки со счетчиком Гейгера-Мюллера и пересчетного устройства Ш-16.

Счетчик Гейгера-Мюллера является детектором высокоэнергетических  или заряженных частиц, рентгеновского и γ-излучения. Действие счетчика основано на возникновении импульсного электрического разряда в газе, наполняющем счетчик (часто это неон или аргон с небольшой добавкой этилового спирта, хлора или брома) при попадании в него детектируемого излучения.

Схематично счетчик и его подключение к пересчетному устройству показаны на Рис.3.

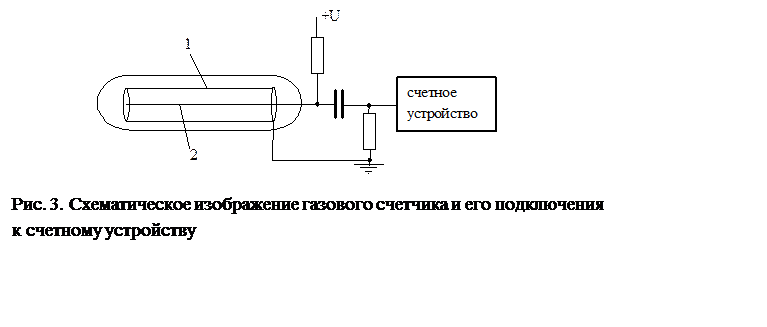Газовый счетчик представляет собой металлический цилиндр 1, играющий роль катода. По оси цилиндра расположена металлическая нить –анод 2. Оба электрода находятся внутри стеклянного баллона, заполненного газом под давлением 100-200 мм рт.ст. Между катодом и анодом прикладывается напряжение 200 – 1000 В. Быстрая частица, попадая в пространство между анодом и катодом, ионизирует газ, вызывая его лавинообразную ионизацию, длящуюся около 10^-2 с и воспринимаемую регистрирующим устройством как отдельный импульс. 

Счетное устройство (Рис.4) представляет собой металлический корпус с расположенных на его лицевой панели шестью индикаторными лампами 1, группой кнопочных переключателей 2 и переключателем полярности сигнала 3. Индикаторные лампы считают импульсы по десятичной системе, отображая (справа налево) единицы, десятки, сотни и т.д. импульсов.