Методическое пособие для подготовки к лабораторным работам по темам: Волновая оптика. Квантовая оптика. Квантовая механика и ядерная физика, страница 29

Из формулы (3.6) видно, что случайную погрешность среднего значения можно уменьшить, увеличивая число измерений в серии.

Конечная цель измерения состоит в том, чтобы определить доверительный интервал, внутри которого с заданной доверительной вероятностью (0,95 в нашем случае) находится истинное значение физической величины X, что выражается записью результата измерения в виде

                                                                      (3.7)

Выражение (3.7) означает, что истинное значение измеряемой величины находится где-то внутри интервала () с заданной доверительной вероятностью.

Приближенная оценка величины s по формуле (3.6) отличается от ее истинного значения из-за ограниченного числа измерений в серии. Это отличие будет тем больше, чем меньше число измерений в серии.[1] По этой причине нельзя принять доверительный интервал просто равным "двухсигмовому" - 2s для используемой нами доверительной вероятности 0,95. Необходимо еще внести поправку, зависящую от числа измерений и расширяющую доверительный интервал. Для этой цели используются так называемые коэффициенты Стьюдента - t_an, приводимые в таблицах (см., например, табл. 1 в конце данного раздела) для разного числа измерений n при различных доверительных вероятностях α. С учетом коэффициента Стьюдента ширина доверительного интервала ∆x вычисляется по формуле

                       Δx = t_an s                                                               (3.8)

Величина ∆x, определенная по уравнению (3.8), характеризует абсолютное отклонение результата измерения от истинного значения и называется абсолютной погрешностью. Абсолютная погрешность еще не дает полного представления о точности проведенных измерений. Например, абсолютная погрешность при измерении двух временных интервалов в 100 с и 10 с оказалась одинаковой и равной 1 с. Ясно, однако, что точность этих измерений различна. Оценить её можно, рассчитав относительную погрешность по формуле

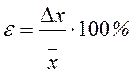                                                                                (3.9)

Относительная погрешность показывает, какую долю составляет абсолютная погрешность от результата измерения и обычно выражается в процентах. В нашем примере для интервала в 100с относительная погрешность составляет 1%, для интервала в 10с - 10%, т.е. точность первого измерения существенно выше.

Таблица 1. Коэффициенты Стъюдента при доверительной вероятности 0,95

n	3	4	5	6	7	8	9	10	15	20	40
tαn	4,30	3,18	2,78	2,57	2,45	2,36	2,31	2,26	2,13	2,09	2,02

ОПРЕДЕЛЕНИЕ ПРИБОРНОЙ ПОГРЕШНОСТИ И ОБЩЕЙ ПОГРЕШНОСТИ В СЛУЧАЕ ПРЯМОГО ИЗМЕРЕНИЯ

Приборные погрешности, являющиеся одним из видов систематических погрешностей, принципиально неустранимы и должны быть учтены при окончательной записи результата измерения.

В зависимости от величины погрешности измерительные приборы подразделяются на восемь классов точности (ГОСТ 8.401-81): 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4. Классом точности прибора называется отношение абсолютной максимальной погрешности прибора (Dx_пр) к верхнему пределу его измерения (x_max), выраженное в процентах

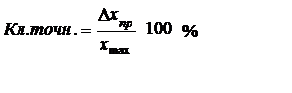                                           (4.1)

Приборы класса 0,05; 0,1; 0,2; 0,5 используются для точных измерений и называются прецизионными. В технике применяются также приборы классов 1,0; 1,5; 2,5; 4. Более грубые приборы обозначения класса точности не имеют. Класс точности прибора обычно указывается на его шкале и в паспортных данных.

Зная класс точности, можно легко определить максимальную приборную погрешность, возникавшую при измерениях данным прибором.

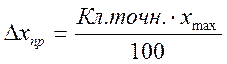                       (4.2)

Завод-изготовитель с помощью класса точности гарантирует лишь верхний предел приборной погрешности, т.е. её максимальное значение. Это значение Dx_пр экспериментатор вынужден считать постоянным при измерениях по всей шкале; конкретная же величина погрешности данного прибора, как правило, неизвестна.

Итак, приборная погрешность одинакова для всех значений измеряемой величины от начала до конца шкалы прибора. Однако относительная погрешность при измерении в начале шкалы будет значительно больше, чем в конце шкалы. По этой причине при эксплуатации многодиапазонных стрелочных приборов (например, в нашем практикуме по электричеству и магнетизму – амперметров и вольтметров) рекомендуется выбирать предел измерения прибора так, чтобы стрелка отклонялась почти на всю шкалу.

Если для прибора или инструмента отсутствуют данные о его классе точности, то максимальную приборную погрешность следует принять равной цене наименьшего деления шкалы этого прибора. Указанное правило связано с тем, что градуировка приборов обычно производится так, чтобы одно деление шкалы содержало от половины до целого значения величины Dx_пр. Так, приборную ошибку линейки с миллиметровыми делениями следует считать равной 1 мм, приборная ошибка секундомера, деления которого нанесены через 0,2 с, составит 0,2 с и т.д. (Следует оговориться, что в некоторых случаях даются рекомендации принимать в качестве максимальной приборной погрешности половину цены деления).

В том случае, если погрешность измерения какой-либо величины складывается из нескольких погрешностей (Dx₁, Dx₂ , ..., Dx_m ), вносимых разными независимыми причинами, то теория погрешностей дает следующий закон их сложения (правило «накопления ошибок»):

                                                         (4.3)